Black Holes and Neutron Stars
Cole Miller
Department of Astronomy and Astrophysics, University of Chicago
The Main Point
Studying neutron stars and black holes gives us
access to exotic realms that we can't explore on Earth.
Abstract
Neutron stars and black holes are among the most exotic objects in the
universe. A lump of neutron star matter the size of a
sugar cube would weigh as much as all humanity, and the
stars have magnetic fields a trillion times Earth's.
Since we can't reproduce such conditions in laboratories,
we have to observe neutron stars with telescopes to
figure out their properties. Recently the Rossi Explorer,
a new X-ray satellite, discovered a remarkable new
phenomenon of neutron stars that strip matter from their
companion stars: their brightness varies almost periodically
more than a thousand times per second. I will describe
how this phenomenon gives us a sensitive new tool to
probe the properties of neutron stars, and how it may
even help us search for black holes.
Intro to Black Holes

A black hole is a region of space in which the
matter is so compact that nothing can escape from it, not even light;
the "surface" of a black hole, inside of which
nothing can escape, is called an event horizon.
The matter that forms a black hole is crushed out
of existence. Just as the Cheshire Cat disappeared and left only its
smile behind, a black hole represents matter that leaves only its
gravity behind.
Black holes are usually formed when an extremely
massive star dies in a supernova.
However, some people think small black holes were formed
during the Big Bang, and that the resulting "mini black holes"
may be in great abundance in our galaxy.
In principle, black holes can have any mass;
black holes formed by stellar death have at least twice the mass
of our Sun. Unlike ordinary things (e.g., rocks), which have a size
roughly proportional to the cube root of their mass, black holes have
radii proportional to their mass. The event horizon of a nonrotating black
hole the mass of our Sun has a radius about 3~km.
Thus, large black holes aren't very dense! A
black hole a billion times as massive as our Sun, such as
is thought to exist in the center of some galaxies, has an
average density just twenty times the density of air.
Black holes, like any gravitating objects, exert a tidal force.
If you approach a black hole feet first, the gravitational force
at your feet is greater than the force at your head.
The tidal force at the event horizon is smaller for larger black
holes: you would get torn to shreds far outside
a black hole the mass of our sun, but at the event horizon of a
billion solar mass black hole the tidal force would only be a
millionth of an ounce!
Strange Facts About Black Holes
- Light bends so much near black holes that
if you were near one and looking away from the hole, you would
see multiple images of every star in the universe, and could
actually see the back of your own head!
- Inside a black hole the roles of time and
radius reverse: just as now you can't avoid going into the future,
inside a black hole you can't avoid going in to the central
singularity.
- If you stood a safe distance from a black
hole and saw a friend fall in, he would appear to slow down
and almost stop just outside the event horizon. His image would
dim very rapidly. Unfortunately for him, from his point of
view he would cross the event horizon just fine, and would meet
his doom at the singularity.
- Black holes are the simplest objects in the
universe. You can describe one completely by just its mass,
spin rate, and electric charge. In contrast, to completely
describe a dust mote you're have to specify the position and
state of all of its atoms, taking at least $10^{16}$ numbers!
- As Hawking discovered, black holes can
evaporate, but only very slowly. Even one the mass of a
mountain will last for ten billion years, and one the mass of
the Sun will only evaporate after $10^{67}$ years.
How Do We Detect Black Holes?
Black holes don't radiate light, and an object that falls inside
a black hole doesn't emit light either, so detecting them can
be challenging.
Just as with neutron stars, if a black hole is in a binary
and it strips gas from its companion, we can detect X-rays from
the resulting accretion disk (see
"Observing Neutron Stars").
The light from accretion disks around black holes looks very
similar to the light from disks around neutron stars, and it is
not always possible to tell with certainty which object lurks
at the center of the disk, although in six cases so far we're
sure that the central object is a black hole.
You can also infer the presence of a black hole in the center of
some galaxies. This is done by observing stars near the center
of the galaxy. If the stars are moving very rapidly around some
unseen object, Kepler's laws can be used to estimate the mass in
the center. In some cases the mass must be at least a hundred
million times our Sun's mass, in a region only a few light years
across. Astronomers are virtually certain that the
only explanation is a black hole, but we lack direct evidence.
The detection of black holes is very difficult and controversial,
and it is being studied actively by many research groups.
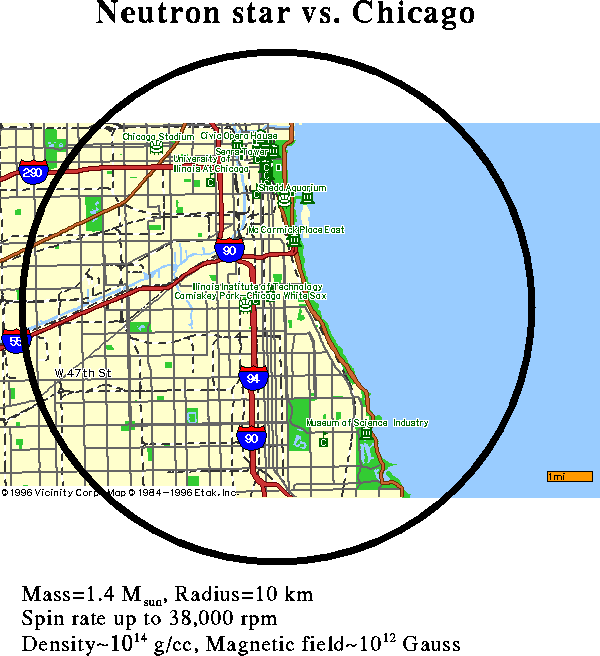
Origin and Scale of Neutron Stars
A neutron star has roughly the mass of our
Sun crammed in a ball ten kilometers in radius.
Its density is therefore a hundred trillion times the density of water;
at that density, all the people on Earth could be fit into a
teaspoon! Neutron stars are born during supernova, and are
held up by neutron degeneracy pressure.
These stars are relatively rare: only
about 10^8 in our galaxy, or one in a thousand stars, so
the nearest one is probably at least 40 light years away.
Neutron Stars and Extreme Physics
- Density at center can be several times the
density of an atomic nucleus, so we can't explore this regime
in laboratories. The properties of this matter are unknown,
and may include such exotic things as enormous conglomerations
of quarks.
- Magnetic fields are a trillion times Earth's,
and more than a million times as strong as can be achieved in
laboratories.
- Matter in the central parts of neutron stars
is thought to be a superconductor, even at a hundred million
degrees!
Neutron stars therefore have states of matter that cannot be
duplicated in laboratories. Study of them helps us test our
theories, and perhaps discover new physics. But how can
we observe neutron stars?
Observing Neutron Stars
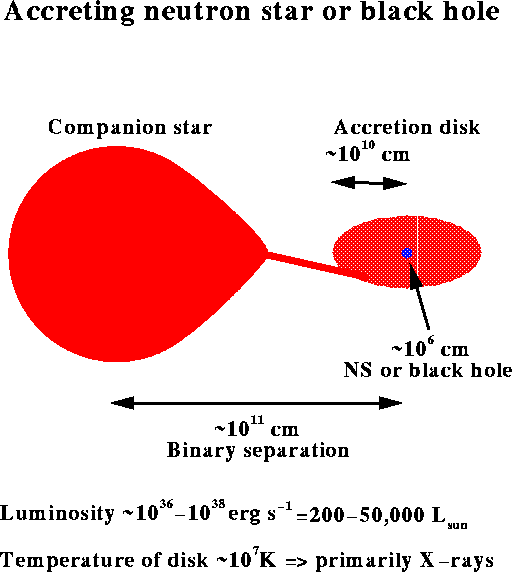
We see a normal star by the light it gives
off during fusion.
Neutron stars are very hot, more than 100,000 K
for most of their lifetimes, so this sounds promising
but most of the energy comes out as X-rays
(not visible light).
Also, neutron stars are so small that at typical
distances they are ten billion times fainter than you can see with
your naked eye, which is too faint for even the Hubble Space
Telescope. We need some other way to see neutron stars.
One way is to see them as radio pulsars.
Another way is if the neutron star is one
member of a binary, in which case the gravity of the neutron
star can strip gas off its companion.
The gas from the companion falls onto the
neutron star, and emits fantastic power in X-rays: as much
as 50,000 times the luminosity the Sun produces.
This is a tremendously efficient way to generate energy.
Dropping a kilogram of matter onto the surface of
a neutron star releases as much energy as a five megaton
hydrogen bomb!
Since the neutron star is a very small target,
astronomically speaking, gas can't fall onto it directly.
Instead, gas spirals around the neutron star, and
friction with itself releases huge amounts of energy in what
is called an accretion disk.
Studying the X-rays from accretion disks can give
us hints about the star: for example, how does matter behave at
extremely high densities?
The Equation of State
As mentioned above, we want to know the
properties of the extremely dense matter in the center of
neutron stars. One way to characterize the matter is by its
equation of state.
The equation of state can be pictured as the relation between
the density of matter and its pressure. Consider a glass of
water. The shape of the water in the glass can be changed
easily (e.g., by sloshing it around), but the volume, and hence
the density, of the water is extremely difficult to change.
Even if you apply a huge amount of pressure to the water, for
example by a piston, the density changes hardly at all; this
is the basis of hydraulic presses. Water may therefore be said
to have a stiff equation of state. In contrast, the
volume of air in an empty glass can be changed easily, with
little pressure, so air may be said to have a soft
equation of state. So, a knowledge of the equation of state
tells us, essentially, how squeezable the matter is.
In the case of a neutron star, knowledge of both the mass and
radius of a particular neutron star would tell us the equation
of state. This is because gravity squeezes the star, and the
more mass the star has the more gravity squeezes it. If the
star has a large radius (meaning, say, 15~km!), it was relatively
successful in resisting gravity and thus has a very stiff equation
of state. If the star has a small radius (say, 8~km), it was
not as successful in resisting gravity and it has a softer
equation of state. We therefore need to estimate the mass and
radius of neutron stars.
Estimating NS Masses and Radii
No easy task, this. Astronomical measurements are often
challenging, because we can't go to a star and experiment on
it. Neutron stars are especially tough, because they are
relatively small and far away: even the closest one would
appear to be the size of a bacterium on the Moon, so we
have to find other ways to determine the mass or radius
of a neutron star.
One way to do this is to use Kepler's laws. If we can figure
out how far two stars in a binary are from each other, and
the duration of their orbital period, we know something about
their masses. Only for neutron stars in binaries do we
have even a rough estimate of the mass, and in only a few of
those cases do we know the mass accurately.
Estimating the radius is much more difficult than estimating
the mass. Unlike the mass, the radius doesn't have any strong
effects on what we can observe. From astronomical observations
alone, neutron stars could have radii from 5~km to 30~km (although
most of that range, all but about 7~km to 20~km, is ruled out
by what we know of nuclear physics).
So, we need some kind of breakthrough in the evidence to allow
us to further constrain the radii of neutron stars.
An Unexpected Discovery
We can only discover what our instruments can detect, so many
times in astrophysics a breakthrough in our understanding has
come from an improvement in instrumental capabilities.
Such was the case when the Rossi X-ray Timing Explorer
was launched on December 30, 1995. Its many outstanding
properties include an unprecedented sensitivity to very rapid
variations of the X-ray intensity of accreting neutron stars, i.e.,
neutron stars stripping mass from their stellar companions.
This led to the discovery of a completely unexpected phenomenon:
fast intensity oscillations, sometimes more than a thousand
times per second!
Kilohertz Intensity Oscillations
Figure 1 shows the X-ray brightness
from one neutron star
system, as a function of time. The intensity goes up and down
nearly 1000 times per second. There are at least 10 known
neutron stars that show this, and we have discovered that:
- The intensity variations are fast, up to 1200
times per second
- For a given neutron star, the frequency of the
variations goes up and down with time: in one case, the variation
can be anywhere from 500 per second to 1100 per second
The dramatic change in frequency means that it can't
be something simple like the spin frequency of the neutron star,
since the star can't easily be spun up or down. However, the common
occurrence of this phenomenon and its other properties mean that
it is telling us something fundamental about the flow of matter
onto neutron stars.
Click to see my proposed explanation of
this phenomenon.
Implications
- The frequency with which the clump goes around
the star is calculated by Kepler's laws: the higher the frequency,
the closer the clump has to be to the star. This limits the
radius of the star.
- When the effects of Einstein's general relativity
are included, it turns out that we also get an upper limit to the
mass of the star.
- The result is that the neutron stars in these
systems must have masses less than 2.2 times our Sun's mass, and
radii less than 17~km. This is the first convincing observational
limit to the radius of neutron stars.
Key Points
- The matter in the center of neutron stars is
incredibly dense, and we can't reproduce it on Earth.
- So, the study of neutron stars can tell us things
about the universe that would otherwise remain forever undiscovered.
- One way to find out about the dense matter of
neutron stars is to determine the equation of state of neutron
stars, which is the relation between their pressure and density.
- The equation of state is known if we know both
the mass and radius of a neutron star.
- But, astronomical observations are indirect: we can't
experiment on stars.
- Neutron stars are particularly difficult, since
they are relatively small and distant.
- Luckily for us, the recently-discovered phenomenon
of rapid X-ray intensity oscillations may allow us, for the first time,
to estimate both the mass and radius of some neutron stars and thus
know their equation of state.
- As it turns out, if we knew the equation of state
of neutron stars, we would also know their maximum mass. This ends
up helping in the search for black holes in our galaxy.
- This phenomenon is still new, and we continue to
learn things about it at a rapid pace, both observationally and
theoretically; these are exciting times!
Glossary
- Accretion disk:
- the pattern of flow of matter from
a normal star to a neutron star or black hole, which is flattened
and thus disk-like.
- Degeneracy pressure:
- a quantum-mechanical phenomenon; fermions, such as electrons
or neutrons, obey Pauli's exclusion principle, so that no two
fermions can occupy the same state. Thus, if fermions are squeezed
together they resist even if there is no temperature and no
energy generation. This resistance to squeezing is degeneracy
pressure.
- Equation of state:
- the relation between the pressure
and density of a given type of matter, which is an indication of how
the matter resists squeezing. If the matter resists squeezing strongly
(e.g., water), the equation of state is stiff; if it resists
squeezing only weakly (e.g., air), the equation of state is soft.
- Event horizon:
- in a black hole, the point beyond
which events cannot be detected. This is the point of no return;
an object that falls inside the event horizon can't get out.
- Kepler's laws:
- rules for the orbital motion of
planets or anything else bound by gravity. The law of most interest
here is that the square of the orbital period is proportional to the
cube of the orbital separation, and inversely proportional to the
mass. Thus, if we see an orbital period, we can estimate the mass
or orbital separation and therefore constrain the mass and radius
of a neutron star.
- Singularity:
- in a black hole, the "center point",
at which densities, tidal forces, and other physical quantities
become infinite. Our current physical theories break down at
this point.
- Tidal force:
- the force an object feels
because of the differential pull of gravity at different distances.
Related Web Resources
-
http://jovian.physics.uoguelph.ca/~droz/inside/
- Black Holes:The inside story. Includes lots of diagrams and
suggestions for further reading. The explanations are thorough and
very readable.
-
http://www.astro.umd.edu/~miller/nstar.html
- Moderately technical guide to various aspects of neutron
star physics
-
http://antwrp.gsfc.nasa.gov/htmltest/rjn_bht.html
- Robert Nemiroff's page on virtual trips to black holes
and neutron stars. Neat animation showing gravitational
light bending!
-
http://physics7.berkeley.edu/BHfaq.html
- Black hole FAQ at Berkeley. Accurate, yet accessible



