Energy determines whether an orbit is bound or not. Circles and
ellipses are the only bound orbits; parabolae and hyperbolae are the
only unbound ones. Note that ![]() orbits (rectilinear or
straight-line orbits) may be elliptical, parabolic, or hyperbolic.
orbits (rectilinear or
straight-line orbits) may be elliptical, parabolic, or hyperbolic.
| Bound Orbits ( |
Unbound Orbits ( |
|||
| Circle | Ellipse | Parabola | Hyperbola | |
| Semimajor Axis: | ||||
| Eccentricity: | ||||
| Distance: | ||||
| Speed: | 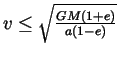 |
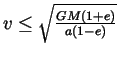 |
||
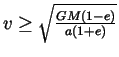 |
||||
(![]() in the limit
in the limit ![]() , i.e., speed at
``infinity'')
, i.e., speed at
``infinity'')