- Do problem #20 from Ch. 3 in the textbook (p. 73), assuming
the orbits of Phobos and Deimos are circular and co-planar.
Neglect the mass and finite size of the moons. Include a sketch
of the situation showing Mars, Phobos, Deimos, and the desired
orbit. This is an example of a Hohmann transfer orbit.
- What is the eccentricity of the transfer orbit?
- What is the minimum time required for the package to get from
Phobos to Deimos?
- At what relative orbital longitudes will the moons need to be
at launch for Deimos to be at the correction position when the
package arrives? How often does this configuration occur (in
other words, what is the synodic period of Deimos relative
to Phobos)?
- Derive an expression for the gravitational potential energy of
a homogeneous sphere of bulk density
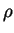 , mass
, mass 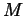 , and radius
, and radius
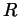 . Hint: consider the contributions of thin concentric
shells of thickness
. Hint: consider the contributions of thin concentric
shells of thickness 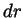 and mass
and mass 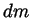 .
.
- Derive a formula for the free-fall gravitational collapse time
of a uniform spherical cloud of density
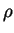 . Hint: the
trajectory of a gas parcel initially at rest at a distance
. Hint: the
trajectory of a gas parcel initially at rest at a distance 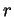 from the center of the cloud can be approximated as a very
eccentric ellipse with semimajor axis
from the center of the cloud can be approximated as a very
eccentric ellipse with semimajor axis 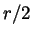 .
.
- Calculate the collapse time for a cloud of H
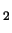 molecules
with
molecules
with 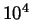 molecules per cubic centimeter.
molecules per cubic centimeter.
- Do problems #21 & 22 from Ch. 4 in the textbook (p. 97).
- Do problems #14 & 15 from Ch. 5 in the textbook (p. 125).
For #14, assume the planetesimal is on a straight-line trajectory
with speed
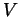 relative to the cloud, and ignore gravitational
focusing.
relative to the cloud, and ignore gravitational
focusing.