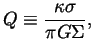
- Compute
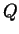 as a function of
as a function of 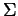 for a disk of identical
1 km radius planetesimals of mass density 2000 kg/m
for a disk of identical
1 km radius planetesimals of mass density 2000 kg/m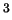 orbiting
the Sun at 1 AU, assuming the velocity dispersion is roughly equal
to the escape speed from one of the planetesimals.
orbiting
the Sun at 1 AU, assuming the velocity dispersion is roughly equal
to the escape speed from one of the planetesimals.
- For what value of
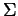 is
is 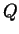 ``critical'' (i.e., equal to
1)?
``critical'' (i.e., equal to
1)?
- Roughly speaking, the scale height of the disk is
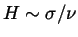 , where
, where 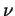 is the vertical frequency. Taking
is the vertical frequency. Taking 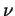 to be
to be 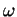 , estimate the volume mass density
, estimate the volume mass density 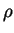 of
the critical disk, assuming it's uniformly distributed. Comment.
of
the critical disk, assuming it's uniformly distributed. Comment.
- Problem #15 from Ch. 6 (p. 153).
- Problem #14 from Ch. 7 (p. 189).
- Using the solution strategy of Homework 1, Problem 3, compute
the minimum required energy as a function of distance to deflect
the comet so that it just grazes the Earth.
- Using the result of Homework 2, Problem 2, compute the minimum
required energy to fully disrupt the comet, assuming an explosive
efficiency of only 0.1% (which is probably optimistic).
- At what critical distance is it more energy efficient to just
blow up the comet rather than deflect it? Express your answer in
Earth radii.