- Jupiter has an estimated emissivity of 0.64. Compute the mean
power in Watts emitted by Jupiter assuming the giant planet is
only reemitting light absorbed from the Sun.
- Jupiter actually glows like a blackbody of effective
temperature 124 K. Compute its emitted power on that basis
(recall, for a blackbody, the emitted flux is
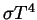 ). Notice that the emitted power is larger that what you
found in part (a)--Jupiter radiates more energy than it receives
from the Sun!
). Notice that the emitted power is larger that what you
found in part (a)--Jupiter radiates more energy than it receives
from the Sun!
- The difference is attributable to the fact that Jupiter is
still contracting and converting gravitational potential energy
into heat. If Jupiter were to convert all its gravitational
binding energy into heat, how long would it take for the giant
planet to contract to a point, assuming it maintained the constant
blackbody temperature of part (b)? (In reality, the contraction
would be slowed to almost zero long before that--why?)
The angular momentum
![]() of a rigid body is related to its
spin vector
of a rigid body is related to its
spin vector
![]() by
by
![]()
![]() ,
where
,
where
![]() is a matrix called the inertia tensor. For
continuous bodies, the elements of
is a matrix called the inertia tensor. For
continuous bodies, the elements of
![]() are given by
are given by
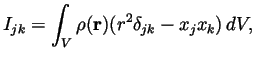
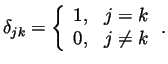
- Compute the inertia tensor for a solid homogeneous sphere of
radius
 and mass
and mass 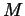 . Hint: compute
. Hint: compute 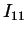 and
and
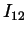 first, notice the pattern, and argue that the entire
matrix reduces to the identity matrix times a single scalar of
form
first, notice the pattern, and argue that the entire
matrix reduces to the identity matrix times a single scalar of
form 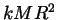 --find
--find 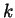 . The quantity
. The quantity 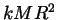 is the
moment of inertia of a solid homogeneous sphere.
is the
moment of inertia of a solid homogeneous sphere.
- Compute the inertia tensor for a solid homogeneous spherical
shell of inner radius
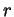 , outer radius
, outer radius 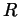 , and total mass
, and total mass
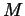 . Hint: all that's really changed from part (a) is the
lower limit of the
. Hint: all that's really changed from part (a) is the
lower limit of the 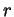 integral--use this to your advantage to
avoid a lot of work! Again, express your answer as
integral--use this to your advantage to
avoid a lot of work! Again, express your answer as 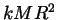 , the
moment of inertia of a solid homogeneous spherical shell, and find
, the
moment of inertia of a solid homogeneous spherical shell, and find
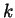 (which will be a function of
(which will be a function of 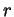 and
and 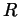 but will still be
dimensionless). Verify the expected behaviour as
but will still be
dimensionless). Verify the expected behaviour as
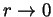 .
.
- Bonus: compute the inertia tensor of a thin
shell of radius
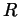 and mass
and mass 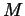 . Hint: use your result
from part (b)--you don't need to integrate!
. Hint: use your result
from part (b)--you don't need to integrate!
- It can be shown that the free precession frequency of a
symmetrical rigid body rotating at frequency
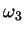 around its
symmetry axis is given by
where we have set
around its
symmetry axis is given by
where we have set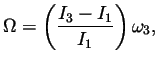
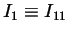 and
and
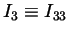 , and
taken the
, and
taken the 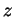 axis to be the symmetry axis (so that
axis to be the symmetry axis (so that 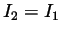 ).1 For the Earth,
).1 For the Earth,
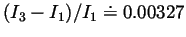 (not surprisingly, this value is close to the
Earth's oblateness
(not surprisingly, this value is close to the
Earth's oblateness
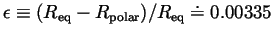 ). Find the
free precession period and compare it to the precession
period of the equinoxes. (It turns out the free precession period
is quite close and probably related to the so-called
Chandler wobble period of the Earth--look it up with
google!)
). Find the
free precession period and compare it to the precession
period of the equinoxes. (It turns out the free precession period
is quite close and probably related to the so-called
Chandler wobble period of the Earth--look it up with
google!)
- Provide the title and a 2-3-sentence description of your
chosen term project (recall the essay is due Nov. 23 and the oral
presentations will be Dec. 7 & 9).