From the kinetic theory of gases, the fraction of particles with
speeds between ![]() and
and ![]() in an ideal gas at thermal
equilibrium is given by the Maxwell-Boltzmann distribution function,
in an ideal gas at thermal
equilibrium is given by the Maxwell-Boltzmann distribution function,
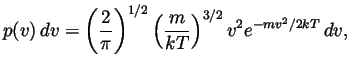
- Verify that this distribution is normalized (i.e., show that
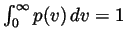 ). What are the units of
). What are the units of 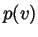 ?
?
- Derive expressions for the most probable speed
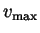 (i.e., the speed corresponding to the peak in the
distribution), the mean speed
(i.e., the speed corresponding to the peak in the
distribution), the mean speed
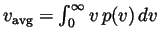 , and the root-mean-square speed
, and the root-mean-square speed
![$ v_{\mathrm{rms}} =
[\int_0^\infty v^2\,p(v)\,dv]^{1/2}$](img11.png) . Show that
. Show that
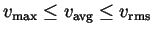 . Evaluate
. Evaluate  at
each of these values.
at
each of these values.
- Plot the distribution functions for hydrogen and oxygen
(
 O) atoms at 900 K, for
O) atoms at 900 K, for 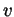 between 0 and 25 km/s. For
what
between 0 and 25 km/s. For
what
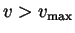 is
is
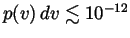 in
each case? Express your answers in km/s, and also in terms of
in
each case? Express your answers in km/s, and also in terms of
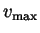 ,
,
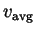 , and
, and
 for
both species.
for
both species.
- Do problem #9 from Ch. 11 (p. 347).
- Also do problem #10.
- Infrared observations of 90377 Sedna show a peak at 88
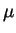 m.
What is the temperature of Sedna? At that temperature, familiar
gases like N
m.
What is the temperature of Sedna? At that temperature, familiar
gases like N and CO
and CO are frozen ices. Helium (He) and neon
(Ne) would still be gaseous. Assuming Sedna has a radius of 800
km and a bulk density of 3000 kg/m
are frozen ices. Helium (He) and neon
(Ne) would still be gaseous. Assuming Sedna has a radius of 800
km and a bulk density of 3000 kg/m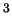 , can this body retain an
atmosphere of He? What about Ne? Comment.
, can this body retain an
atmosphere of He? What about Ne? Comment.