Clickers
nota bene:
PHYS103 MUST be taken in the same semester as PHYS102 if you're trying to fulfill a science lab course general education requirement (DSNL).
Do Participation #1 and Homework #1 on ELMS!
Buy your clicker at the bookstore. Make sure it's one of the right ones: if you're not buying an app for your mobile device, the RF-LCD is the recommended choice (click on the pictures at right to see up close). And register your clicker here

RF-LCD response card |

RF response card |

XR response card |
Some Basics
Fun with powers of 10 in physical scale
Here's a website for playing with wavelength and frequency to get a sense of scale. It's somewhat abstract.
Learn your prefixes. It's not as unfamiliar as you might think (okay, except for pico and tera; and the funny "mu" for micro).
|
|
The website on Scientific Notation should help those who need a refresher, or those who didn't understand the first time they saw it.
By the way, try timing the wave in the box to the right. The scale on the horizontal axis goes from 0 to 12 m.
For more fun with waves (i.e., to see the difference between transverse waves like light and longitudinal waves like sound), you can try these applets. Scroll down to the section on waves, and check out transverse and longitudinal. One important thing is that you can change the frequency, but the velocity of the wave is constant so what happens to the wavelength? Experiment!
But Does It Have a Good Beat?
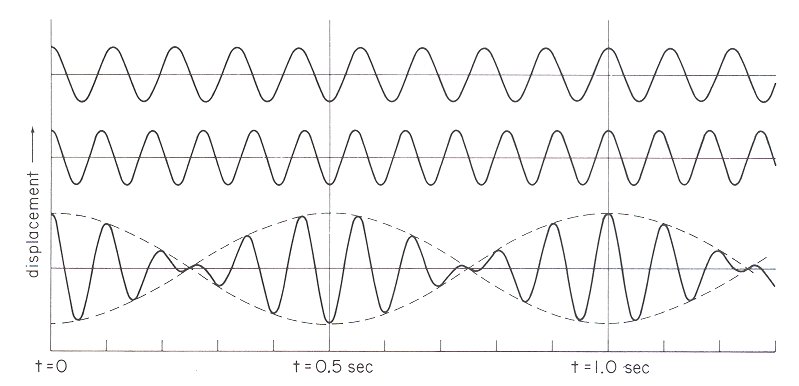
Here's a great beats applet to play with so you can see what happens when you add two waves together, i.e., superposition. The graph you see is two waves "travelling" in space to the right. What do you notice about the wavespeed as you change frequency? (It's constant!) Try these various settings for the two frequencies:
- red = 15 Hz, green = 16 Hz
- red = 2 Hz, green = 3 Hz
(note same beat envelope as above!) - red = 8 Hz, green = 8 Hz In Phase
- red = 8 Hz, green = 8 Hz Out of Phase
On the Wavelength of Violins and Cellos.
I've asked how the wavelength of a violin note was related to the wavelength of the sound it produces. Now I keep saying that "the velocity of a wave (really its speed) is fixed by the medium." This is a subtle point because you have to recognize there are TWO media: the tense string which vibrates (standing waves: we'll get to that soon) and the air which vibrates (sound waves).
On the string, the tension sets the velocity of the string vibrations: when you change the tension, the velocity changes. The wavelength of the string vibrations is fixed by the length of the string (this is a property of standing waves and we'll cover that soon). So the frequency of the string vibrations is equal to the velocity (set by the tension) divided by the wavelength (set by the length).
fstring = vstring/λstring (1)
Now let's talk about the air. The frequency with which the string vibrates is the frequency the sound wave will have because the compression in the air is caused by the vibrations of the string. (Recall my mantra in class, "The frequency of the sound is determined by the physical system producing the sound.")
fstring = fsound (2)
But, the velocity of the sound wave is set by its medium (air), so the wavelength of the sound wave is the velocity of sound in air divided by the frequency of the sound.
λsound = vsound/fsound = vsound/fstring (3)
So the wavelength of the sound is related to the wavelength of the violin strings and the velocity of the string vibrations, which I can change by turning a peg and loosening or tightening the tension in the string.
λsound = vsound/fstring = ( vsound/vstring )λstring (4)
Whew. Reread this slowly until it makes sense. Maybe even do the algebra yourself a couple times.
The important thing is that (so long as I don't press down with my fingers and change the note) an open note on the violin has a fixed wavelength so λstring is constant, and the velocity of sound in the air vsound is constant. So looking at equation (4) above, the wavelength of the sound wave produced by an open string on the violin will only vary with the velocity of the string vibration. Okay, looking at any of the equations above, answer this question:
Assuming that when I tighten the string the note sounds higher pitched, how are the velocity of string vibrations vstring related to the tension of the string? In other words, does the velocity of the string vibration increase or decrease when I tighten the string?

On Drums and Bridges
Here is an excellent website showing the basic "drumskin" modes of vibration. Although the explanation is arguably a little too technical for this class, the pictures are worth a thousand words (and a couple dozen formulae).
Remember for strings and tubes that each mode is a higher Nth harmonic of some fundamental mode. Notice that since drumskins are two-dimensional, there are two parts of the fundamental modes. This is not a coincidence. So we list them separately: (M,N). Figure 3-23 in our textbook regarding bridges imply that there are two parts to the mode (the two parts of the figure show the (1,1) mode at two times during its cycle): one harmonic based on the narrow dimension of the bridge and one on the long dimension of the bridge. If you watch various footage on youtube, some of the pictures only show one mode being excited (the narrow dimension). But when both modes are excited, the twisting ("torsional mode") is too much for the structural strength of the concrete and thar she blows.
Also note the comment that the guy who left his car is walking back along a node: the painted divide in the middle. Watch for a few cycles and you'll notice that the node doesn't move. That's why it's a node.

Logs
Logarithms seem to stymie people, but they are no worse than 'regular' numbers. Here are some online tutorials if you really are stuck. The main thing is, you don't actually need a calculator unless you're trying to be really precise!
log(a)=b means that 10b=a
A LOGARITHM IS AN EXPONENT! In other words, the logarithm of a number [log(a)] is the exponent you would need to slap on a ten [10b] to get that number [a]. That also means that b = log(10b)=log(a) and 10b=10log(a)=a. We're not going to worry about bases other than 10, but the principle is the same.Rock On, Man! (Hunh? Can't Hear You, Man!)
Click here (later this semester) for an outline of how to solve the "Rock Concert" problem. It's not enough to learn how to do the math; it's important that you develop a sense that decibels are shorthand for extremely large changes in actual energy intensity in the sound.
Here's a great site to check your answer. Ignore the fact they call it the 1/r law instead of 1/r2 and just scroll down to their little app. (It's 1/r for them because they're misinterpreting logs.) If you plug in r1 = 10 feet and Loudness1 = 120 dB and Loudness2 = 80 dB, it spits out the right answer. To get full credit from the grader, you should show how to do it without this app!
Click on the image to see how the ear hears logarithmically up close and personal. From: Juan G. Roederer, The Physics and Psychophysics of Music
Click on the image to see Just Noticeable Difference (in frequency) up close and personal. From: Juan G. Roederer, The Physics and Psychophysics of Music
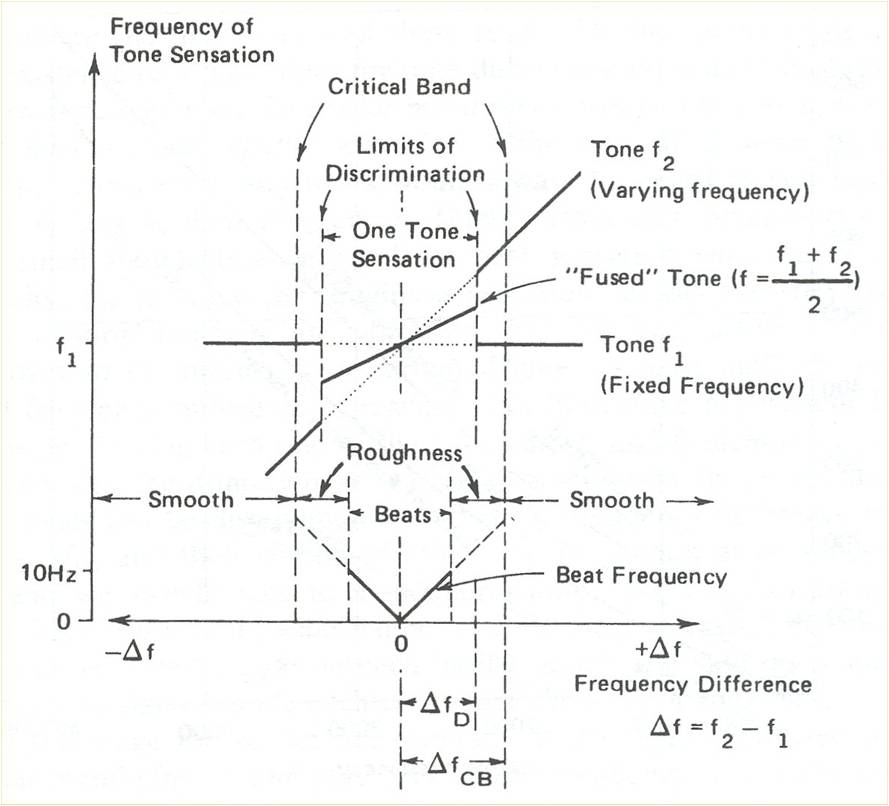
Click on the image to see the critical band based on holding one frequency constant (f1) and adjusting the second frequency (f2) up and down from f1. From: Juan G. Roederer, The Physics and Psychophysics of Music
The Ear!
Chapter 6 links of interest:
- OSHA hearing regulations
- Cochlear Implant Awareness Foundation
- University of Melbourne Bionic Ear Institute
- more info
- Advanced Bionics (a manufacturer)
Acoustics!
Some fun with Flutter Echoes.
I Am Sitting in a Room by Alvin Lucier, 1969. Guaranteed to cure insomnia; an interesting exercise in figuring out room resonances. If you listen to the end, note that the resonances bear a rough relationship to each other as harmonics!
How to make a violin from scratch.
gravicembalo col piano e forte
and others...
The action on a piano. You can "play" it here. You are responsible for understanding: the hammer (why is it covered in felt?), the key, the damper and, of course, the string.
Why do piano tuners "stretch octaves"? (See diagram to the right.) They actually sharpen notes higher than a reference octave (around the middle of the piano) and flatten notes lower than that octave.
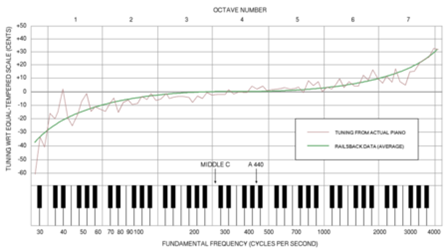
Click on the image to see it larger.
A tour of musical instruments
Please let me know if any links aren't working!It's always dangerous to post Youtube videos here as they can change quickly (such as get yanked), but here are some fun ones used in class:
Shakuhachi flute used in class to demonstrate combining a fipple with an embouchure.
The aptly named Bombarde (with a VERY high pitched bagpipe in the background)
Modern "Celtic Rock" with a Bagpipe
Macedonian pipes, worth a chuckle. Makes you wonder: what are the drone pipes coming out of?
And if you want to freak out your roommate, you, too, can learn to Tuvan throat sing!
The Serpent, a difficult "brass" instrument to play; tone quality with fingerholes (instead of valves) definitely strange to modern ears...
...much like the Cornetto, a similarly odd sound.
Mute (one kind)
Mute (another kind)
Viola da gamba, a fretted, bowed instrument. What does gamba mean? Hint: the other kind is viola da braccio and braccio is related to the English word for "embrace"...
For those interested in a niche career, consider combining throat singing with the igil.
Lute! (no, not the $ kind; that's loot). Note the sympathetic strings (which can also be plucked rather than be passively resonant...)
Did someone say oud?
Japanese Koto.
And the lovely Sitar. Note the frets are not laid out in the same way a guitar's are. Why is that, d'you suppose?
The banjo has, essentially, the makings of a snare drum attached instead of a resonant box like the others above.
I can't resist this one. Redgrass!
Not discussed in class is this classic from your elementary school days: the autoharp. I ought to give extra credit for surviving listening to this particular track (but I won't).
An amazing example of playing the violin pizzicato; more amazing because she's alternately plucking and bowing! After she finishes the pizzicato section, she plays overtones - this is done by not pushing the string all the way down so that the dominant note you expect is not nearly as loud as the octave higher (N=2).
And you can hit strings, too, as with this hammered dulcimer... ...which leads, naturally, to the earliest protopianos, such as the clavichord (also here) with its sharp-edged hammers and tinny sound and the harpsichord (also here) with its plucked strings (allowing for very little control on dynamics).
And here, a little joke. The "harp" made out of a piano frame that Harpo pulls out of the broken piano is not actually strung like a piano since the notes aren't doubled up (or tripled in the higher register). Note the number of pegs is right: they're just not all used!
Finally, here is something you probably shouldn't do to a good piano
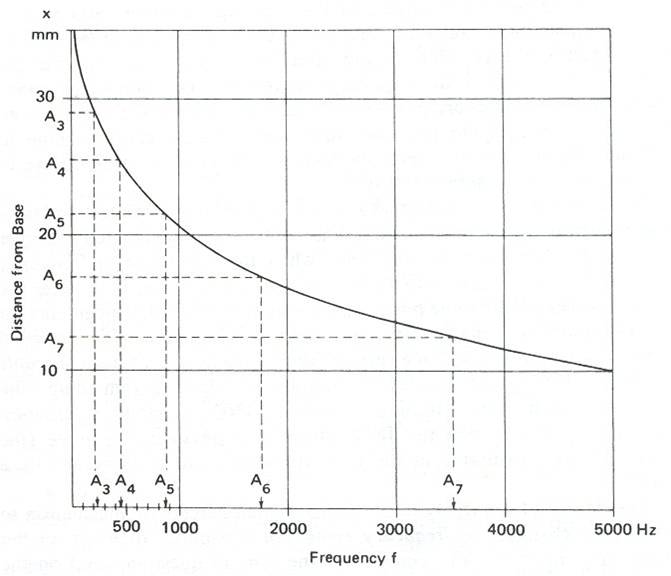
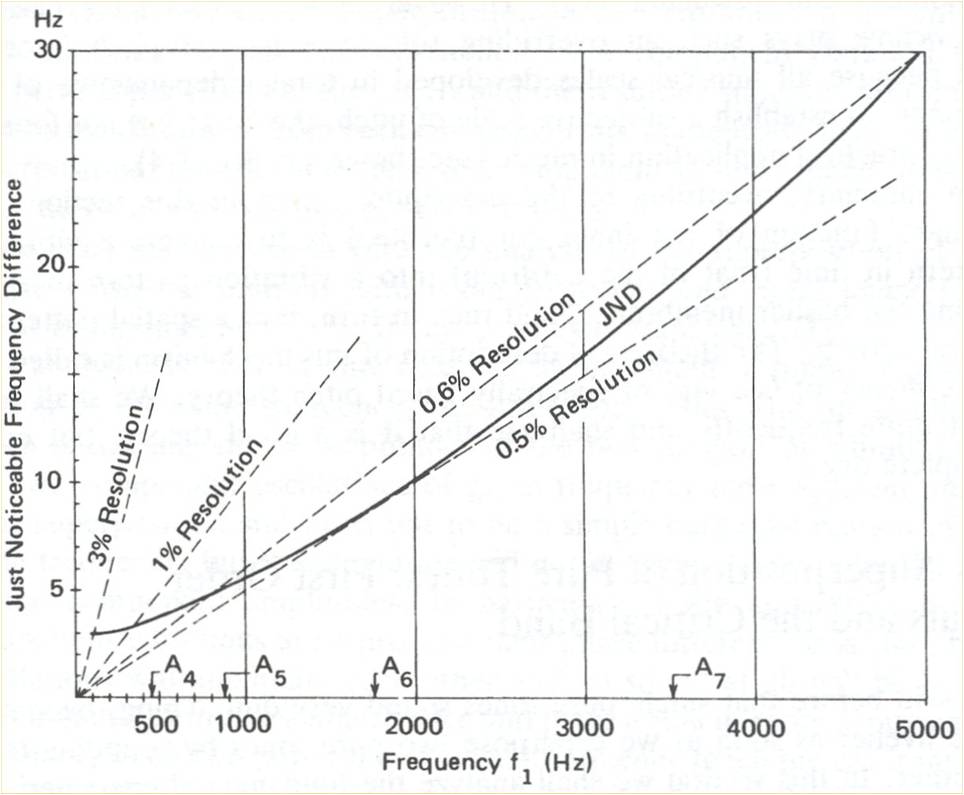
 Back to
main class description webpage
Back to
main class description webpage