


Next: About this document ...
ASTR615 Fall 2015 Problem Set #3
Due Oct 21, 2015
Topics for this problem set include round-off error and linear
algebra.
- As an example of an unstable algorithm, consider integer
powers of the ``Golden Mean''
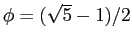 . It can be
shown that
. It can be
shown that
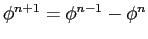 , i.e. successively
higher powers of
, i.e. successively
higher powers of 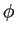 can be computed from a single subtraction
rather than a more expensive multiply. Write a single-precision
program to compute a table consisting of the columns
can be computed from a single subtraction
rather than a more expensive multiply. Write a single-precision
program to compute a table consisting of the columns 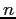 ,
, 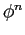 computed from the recursion relation, and
computed from the recursion relation, and 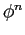 computed directly
(i.e.
computed directly
(i.e.
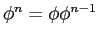 ), for
), for 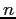 ranging from 1 to 20. Is
the round-off error random? What happens in double precision?
ranging from 1 to 20. Is
the round-off error random? What happens in double precision?
- Write a program to compute the instantaneous spin period of a
rigid body made up of identical, discrete, point particles. Use the
fact that the angular momentum is
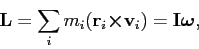 |
(1) |
where 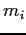 is the mass of particle
is the mass of particle 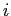 ,
, 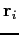 and
and
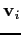 are its position and velocity vectors with respect to
the centre of mass,
are its position and velocity vectors with respect to
the centre of mass,
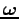 is the spin vector, and
is the spin vector, and
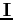 is the inertia tensor
is the inertia tensor
where 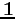 is the unit
matrix. [For continuous bodies the summations are replaced
by volume integrations and the particle masses become a mass
density. In the present case the
is the unit
matrix. [For continuous bodies the summations are replaced
by volume integrations and the particle masses become a mass
density. In the present case the 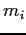 's can be omitted
entirely since the particles are identical.]
Write a program to solve Eq. (
's can be omitted
entirely since the particles are identical.]
Write a program to solve Eq. (![[*]](crossref.png) ) for
) for
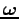 (feel free to use the routines in
Numerical Recipes).
The spin period is then
(feel free to use the routines in
Numerical Recipes).
The spin period is then
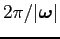 .
.
- Test your code by reading the data file
http://www.astro.umd.edu/~ricotti/NEWWEB/teaching/ASTR415/ps2.dat
which is in the format 
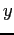
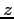
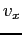
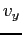
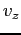 (i.e. 6
values to a line separated by white space). The units are mks
(SI). What is the spin period in hours?
(i.e. 6
values to a line separated by white space). The units are mks
(SI). What is the spin period in hours?
- Make a graphical representation of the body using your
favorite graphing package. If you use 2-D projections, be sure to
include enough viewing angles to get a complete picture.



Next: About this document ...
Massimo Ricotti
2015-10-06
![[*]](crossref.png) ) for
) for
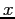
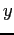
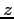
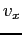
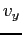
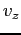 (i.e. 6
values to a line separated by white space). The units are mks
(SI). What is the spin period in hours?
(i.e. 6
values to a line separated by white space). The units are mks
(SI). What is the spin period in hours?