Current students should click on "Class Websites" on the left. Those interested in my teaching philosophy should click on "Hire Me!" on the left and look at my teaching statement.
| Looking for someone who can inspire students? Looking for a physicist who believes and then proves that anyone can learn physics? Is your department getting bad looks from the Dean because your Research One faculty keeps failing everyone in Physics 101? Do your course evaluations start out with, "I hate physics"? Sounds like you need to hire me to spin up your undergraduates in or outside of the field! Look no further! There I was, a typical postdoc at DAMTP on a typical, sunny, English day. Click on the stunning picture to the right for more details (cv, etc.) about the exciting possibility of hiring me! |
|
|
|
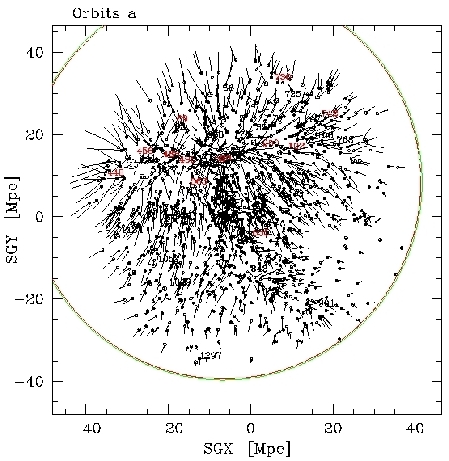
| Numerical Action Methods are designed to simulate the past orbits of known objects. In a sense, they act like N-body simulations running backwards in time using actual galaxy positions and/or velocities today as "initial" conditions. One crucial difference is that they solve for all timesteps of the orbits simultaneously and exactly. While they cannot account for energy loss or gain to any specific halo, merger histories, etc., we have experimented with "mass growth" methods whereby halos gain the mass they have today in some parametric way from the background to great effect. Here is a plot showing the NAM recreated orbits for 1300+ objects within 3000 km/s (translation for cosmologists: sizeable halos within z=0.01 = 30/h ~ 41 Megaparsecs ); many galaxies have been grouped together to simplify tidal effects on our local group; the short, straight orbits signify a low choice of mass to light for this run. |
|
|
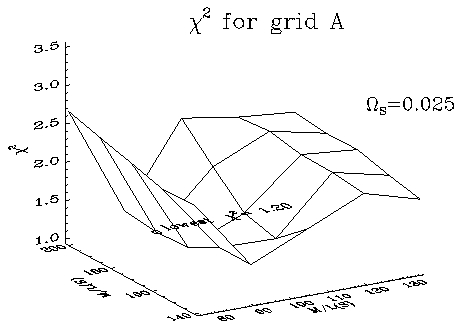
Using galaxy group catalogs from work by B. Tully and collaborators, we have shown the constraining power of NAM on the local Mass-to-Light values for Spirals and Ellipticals separately. On the left we show an example of a three-parameter chi2 analysis: one parameter, ΩS, the density of smooth matter not in halos, is shown fixed; the other parameters are mass to light for elliptical and spiral galaxies. This example was on a small subset of the catalog shown above. Currently we are working on using NAM for a large catalog (~40 Mpc for cosmologists, 3,000 km/s for astronomers, z=0.01 for both) to "generate" initial conditions for use with an N-body program such as Volker Springel's GADGET code. In this way, we can better simulate the local universe; the ultimate "Constrained Simulation". |
| In a past life, well, a year or so ago, I was at the Department of Mathematics and Theoretical Physics (DAMTP for short) in the Relativity and Gravitation Group. There I worked on optimizing large scale weak lensing surveys by combining other large scale information; characterizing selection effects in Sunyaev-Zel'dovich experiments on peculiar velocity statistics; and a careful critical analysis of unified dark energy-dark matter models. Other previous work (detailed below) has included (1) optimizing Cosmic Microwave Background (CMB) analysis methods, (2) Coding up a maximum likelihood estimator for CMB polarization modes, (3) estimating how much galaxy cluster peculiar velocities constrain cosmological parameters using linear theory, modified linear theory and simulations, (4) modeling point source contributions to the kinetic SZ effect, and (5) writing IDL code to make pretty pictures of hydrodynamic clusters. But everything in cosmology is fascinating, and I've been known to dabble in more esoteric stuff (well, esoteric to an Astronomer, anyway) such as quintessence, brane worlds and quantum cosmology. I'm guilty of other physics interests such as the "Arrow of Time" problem and (like all good theorists) grand unification. |
|
The kinetic Sunyaev-Zel'dovich effect is the doppler shifting of Cosmic Microwave Background photons by the hot plasma in the center of very large mass haloes (~1014 Msol) has to potential to provide a catalog of redshift-independent galaxy cluster velocities. Using these velocities to constrain Ωm seems natural since the velocities are responding to the amount of matter in the universe. Based on linear theory, the constraints on Ωm from 1000 clusters are a few percent given a noise of about 100 km/s. However, because the kSZ only occurs for a specific mass cutoff, the selection bias greatly reduces this constraining power. Using N-body simulations, I show in a recent paper that for a concordance universe, the dependency on Ωm is close to nil for a constant value of sigma8 at very recent redshift. And at higher redshift, the dependency is reverse to what linear theory suggests. |
|
Peculiar velocities trace the density field in a great, non-biased way (at
least in linear theory!). Recent excitement about using galaxy cluster
peculiar velocities is motivated by their possible uses to reconstruct
(large modes of) the real-space potential. Our paper details how many
cluster
velocities
we need from a given observational volume to determine modes based on
limitations from (1) confusion between dark matter and gas velocities and
(2) what we call the "undersampling noise" in that cluster-cluster
separation is larger than the pre-collapse radius of a typical cluster.
In principle, weak lensing provides complementary information about the
gravitational potential (the transverse modes as opposed to the radial
modes from velocities), but we show that such information is very weakly
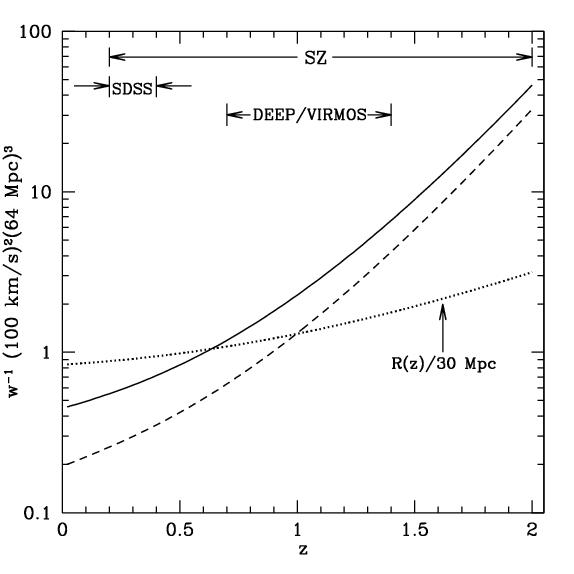
constraining (no pun intended). The image to the right shows the
noise due to both limiations listed above (solid line) for particular
redshifts (note the redshift
dependence of the undersampling noise (dashed line)). The dotted line
represents (half) the typical distance between clusters since: 4/3 pi R3 n(z) = 1 The ranges at the top reflect three theoretical "reference" observational regimes. |
|
|
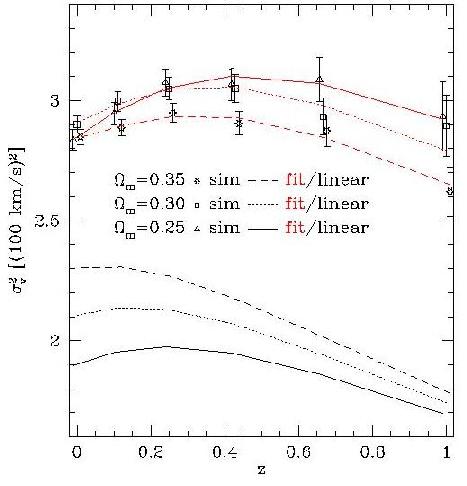
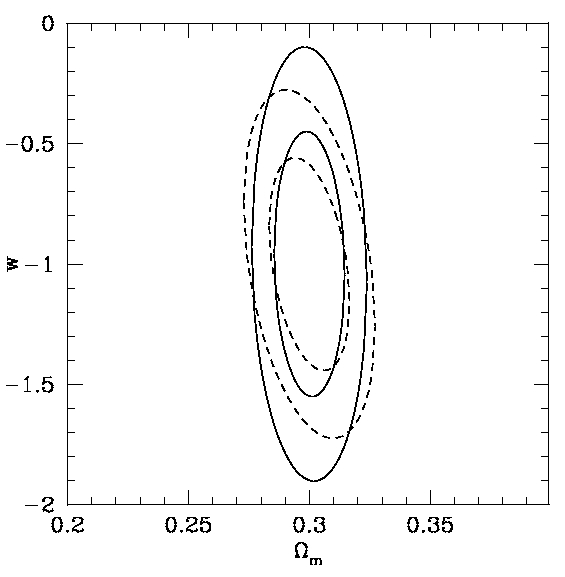
On the left, we show how well galaxy cluster peculiar velocities from linear theory might constrain Ωm and the dark energy equation of state parameter, w. These 1- and 2-sigma curves are based on a Fisher matrix analysis of 820 clusters. The dashed lines are for 820 sparsely sampled clusters from z=0.1 to 1.0 from an artificial grid; the solid lines for 820 neighboring clusters near z=1.0 based on the Virgo Consortium's Lightcone Simulation Cluster Catalog (link to our paper). These parameter forecasts are very optimistic and do not include selection effects. My current velocity paper shows that the mass selection bias effects in a Sunyaev-Zel'dovich (SZ) experiment will alter the Ωm dependency greatly. There are other issues with realistic data such as non-linear evolution, temperature profiles, etc. Regardless of these complications, the constraints in parameter space are related to the time derivative of the growth factor, dD/dz, and therefore should be complementary to parameter constraints from dN/dz (per steradian) type cluster statistic measurements, CMB measurements, and supernovae type IA measurements. Upcoming SZ surveys and serendipitous SZ detections from Planck promise to create a useful SZ cluster survey catalog; followup multiwavelength (in sub-mm) and X-ray astrometry and redshift followup have the potential for attaining unprecendented accuracy in peculiar velocity data. I hope to develop the tools for using that data for cosmology. |
| On the right, we show how well hierarchical decomposition can be expected to recover the angular power spectrum; the "exact" method shown for comparison refers to MADCAP. The solid line comes from CMBFAST using Lambda-CDM model parameters and was in turn used by HEALPIX to generate a map of the whole sky. The hierarchical decomposition methods have incredible speed advantages (link to our paper) over more exact methods with minimal loss of information which will become a crucial issue for upcoming megapixel CMB missions such as the ongoing WMAP and upcoming Planck satellites when exact methods become unreasonably computer intensive. |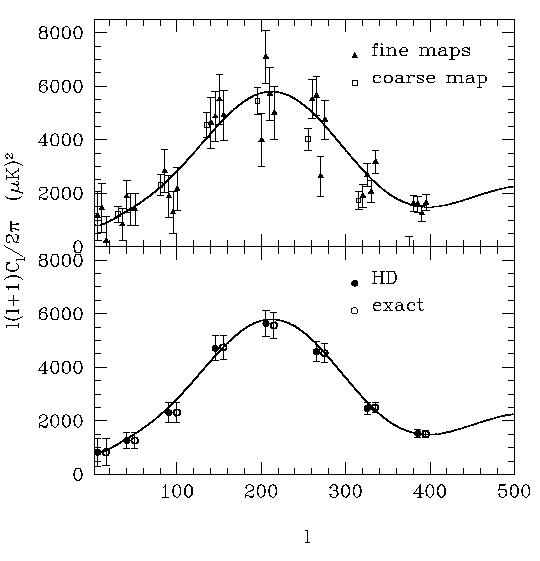 
|
|
The background wallpaper is a Hubble image of galaxy cluster Abel 2218 (for full view click here) which is so massive that it acts as a magnifying and distorting strong lens on the galaxies behind it. The bright yellow galaxies are in the cluster itself, while the bluer elongated images are from galaxies far behind the cluster. This is an example of strong lensing. But even a less massive cluster will cause weak lensing, which can only be ferreted out by statistics. By combining weak lensing estimates of the shear caused by an overdensity with the line of sight estimated mass it may be possible to reconstruct the potential of such overdensities. |
|
So you might be wondering, "What's the otter doing up there at the top of your webpage? And why are you wearing a fez?" To which I reply, "The otter's eating abalone, of course. And I claim fezzes will be the next black after shawls depart (and none too soon!)." ***Update*** Shawls have departed. Rubber fezzes have arrived! |
|
You can email me at:
peel(at)astro.umd.edu
[the (at) is to be replaced by an @;
writing it this way helps deter spam] Snail-mail me at: Alan Peel Department of Astronomy University of Maryland College Park, MD 20742-2421 USA tel: (301) 405-6647 |
Welcome! I am a postdoc at the