Fabry-Perot tunable filters operate on similar principles to narrow-band interference filters. In a single-plate interference filter, the interference occurs in the interior of a solid plate, where the two sides of the plate act as reflective surfaces. In a tunable filter, the interference arises in the air gap between the surfaces of two separate plates.

Fabry-Perot tunable filters offer several advantages over their single-plate counterparts.

1. Tunable filters are tunable in wavelength space. By making small changes in the air gap between the two plates, one can change the transmitted wavelength.
2. Tunable filters are tunable in bandpass. By making large changes in the air gap between the two plates, one can change the width of the transmission profile.
3. Tunable filters provide very narrow bandpasses. Through rejection of significant sky and/or continuum emission (compared to conventional narrow-band filters), tunable filters can significantly improve observing efficiency for reaching a desired signal-to-noise ratio.
4. Tunable filters can switch between two wavelengths on short timescales. Coupled with charge-shuffling on the CCD, this allows the user to correct for time-varying observational effects, including atmospheric transmission and sky brightness. It also allows for differential imaging on short timescales.

Alternatively, tunable filters function as wide-area, low-resolution spectrometers. From this perspective, a tunable filter achieves a significant efficiency advantage over conventional long-slit spectrographs (Jacquinot 1954).

Fabry-Perot tunable filters have been used for a wide range of applications, including (but not limited to) the following:

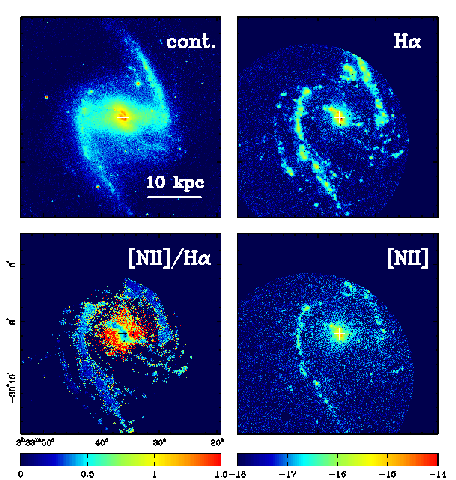
• Emission- and absorption-line maps of galaxies
• Emission-line ratio ("excitation") maps of galaxies
• Searches for warm, diffuse gas on the outskirts of galaxies
• Imaging of Galactic line-emitting sources
• Wide-field surveys for high-redshift line-emitting galaxies
• Suppression of quasar light in Lyα forest troughs
• Tracking of stellar variability using differential imaging

For general Fabry-Perot physics, refer to an optics textbook (e.g., Hecht's Optics) or this succint Wikipedia entry. For more details on tunable filters, see the references given below. We summarize here the important points.

For Fabry-Perot etalons to operate as tunable filters, the plate spacing must be small. This ensures that the monochromatic spot at the center of the field of view is large, or equivalently the spectral resolution is low. The monochromatic, or Jacquinot, spot is defined to be the region over which the change in wavelength does not exceed √2 times the etalon bandpass. For a given wavelength, small plate spacing translates into low interference orders.

More specifically, the diameter of the Jacquinot spot is given by

  DJ = 2√(2√2) F / √(nN)
     ~ 3.3636 F / √(nN)

  where F = camera focal length (in pixels)
        n = order of interference
        N = etalon finesse (see discussion below)

For a given order, the monochromatic spot depends on wavelength only through the finesse. (The finesse, which we discuss below, depends on the transmission of the plate coatings.) However, as we discuss in the next paragraph, order is proportional to plate spacing d, so that D_J ~ 1/√d.

The transmitted wavelength at any point on the etalon is governed by interference principles: n λ = 2 d cos θ, where n is the interference order, λ is the wavelength, d is the effective plate spacing (including any optical effects due to the coating or air gap -- these may change with wavelength), and θ is the angle of the incident light with respect to an axis perpendicular to the plates. The transmitted wavelength can be modulated by either (a) changing the plate spacing d or (b) changing one's radius with respect to the optical axis, represented by cos θ. (At the CCD, the θ dependence translates into a radial dependence of wavelength; the optical axis is at the center of this radial pattern.)

Interference orders are separated by a free spectral range (FSR). Each transmission peak is characterized by an Airy profile. The ratio of the free spectral range to the instrumental resolution (in terms of the effective bandpass, defined as the profile area divided by its peak) is the effective finesse. In a perfect system, the effective finesse is equal to the reflective finesse, which is a function of the etalon plate coatings. However, irregularities in the plate surfaces and coating thicknesses, as well as deviations from perfectly parallel plates, degrade the effective finesse, and hence the efficiency of observing.

In summary, the interference equation governing the etalon is

  n λ = 2 d cos θ

  where n = order of interference
        d = plate spacing
	θ = angle of incident light with respect to the optical
        axis (θ = 0 at the optical axis)

The equations governing the instrumental profile are as follows:

• Expressed as functions of wavelength,

     FSR(λ) ≅ λ / n ≅ λ2 / 2 d
    FWHM(λ) ≅ FSR(λ) / Finesse ≅ λ / [n Finesse] ≅ λ2 / [2 d Finesse]
  
    where FSR = free spectral range
          FWHM = full width at half maximum
  	Finesse ≅ FSR / FWHM
  

• Expressed as functions of plate spacing,

     FSR(d) = λ / 2
    FWHM(d) ≅ FSR(d) / Finesse ≅ λ / [2 Finesse]
  

The wavelength dependencies are summarized as follows:

• On the optical axis, for effective plate spacing d,

    λ = A + B z
  

  where z = z(d) represents voltages applied to the etalon by the CS-100 and is the variable read by the IMACS computer. It is a linear function of plate spacing d:

    d = E + G z,
  
    where E = n A / 2
          G = n B / 2.
  

  A and B thus vary from order to order. By substituting for n using the interference equation, we also see that A and B vary linearly with wavelength for a given plate spacing.

• Off the optical axis at radius R:

    λ(R) = λ(0) / √(1 + R2/F2) = (A + B z) / √(1 + R2/F2)
  
    where F = focal length of the camera.
  

  Note that wavelength decreases with increasing distance from the optical axis.

Bland, J., & Tully, R. B. "The Hawaii Imaging Fabry-Perot Interferometer (HIFI)." 1989, AJ, 98, 723

Bland-Hawthorn, J., & Jones, D. H. "TTF: A Flexible Approach to Narrowband Imaging." 1998, PASA, 15, 44

Jacquinot, P. "The Luminosity of Spectrometers with Prisms, Gratings, or Fabry Perot Etalons." 1954, J Opt Sci Amer, 44, 761

Jones, D. H., Shopbell, P. L., & Bland-Hawthorn, J. "Detection and Measurement from Narrow-band Tunable Filter Scans." 2002, MNRAS, 329, 759

Taylor, K., & Atherton, P. D. "Seeing-Limited Radial Velocity Field Mapping of Extended Emission Line Sources Using a New Imaging Fabry-Perot System." 1980, MNRAS, 191, 675

The TTF (Taurus Tunable Filter), formerly on the Anglo-Australian Telescope (see also articles listed above)

Fine Guidance Sensor - Tunable Filter, on the James Webb Space Telescope (see also these articles)

OSIRIS (Optical System for Imaging and Low-Intermediate-Resolution Integrated Spectroscopy), on the Gran Telescopio Canarias (see also these articles)

The Prime Focus Imaging Spectrograph, on the South African Large Telescope (see also these articles)