

Welcome to my neutron star page! I need to emphasize that the stuff I have here represents my opinions, and errors aren't the fault of those patient pedagogues who tried to cram this information into my head. I'll try to indicate when there is a dispute in the community, but I won't always be successful, so don't use only this page to study for your candidacy exams! For those with serious interest in neutron stars and other compact objects, an excellent reference is "Black Holes, White Dwarfs, and Neutron Stars", by Stuart Shapiro and Saul Teukolsky (1983, John Wiley and Sons).
For those who want a quick intro to selected cool things about neutron stars and black holes, check out a poster I made for a science fair at the University of Chicago. If you'd like more detail about quasi-periodic oscillations in particular, I wrote a pedagogical review based on my summer school lectures in Dubna, Russia, in August 2004. Here are the Postscript and PDF documents.
I also have a link to some questions I have received about neutron stars, and my answers. Here are the topics in this page:
Getting started on neutron stars
Neutron stars are the collapsed cores of some massive stars.
They pack roughly the mass of our Sun into a region the size of
a city. Here's a comparison with Chicago:
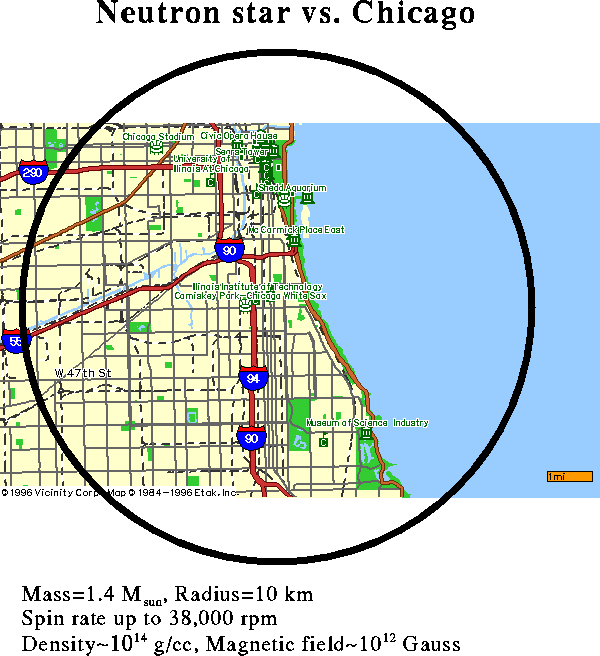
At these incredibly high densities, you could cram all of humanity into a volume the size of a sugar cube. Naturally, the people thus crammed wouldn't survive in their current form, and neither does the matter that forms the neutron star. This matter, which starts out in the original star as a normal, well-adjusted combination of electrons, protons, and neutrons, finds its peace (aka a lower energy state) as almost all neutrons in the neutron star. These stars also have the strongest magnetic fields in the known universe. The strongest inferred neutron star fields are nearly a hundred trillion times stronger than Earth's fields, and even the feeblest neutron star magnetic fields are a hundred million times Earth's, which is a hundred times stronger that any steady field we can generate in a laboratory. Neutron stars are extreme in many other ways, too. For example, maybe you get a warm feeling when you contemplate high-temperature superconductors, with critical temperatures around 100 K? Hah! The protons in the center of neutron stars are believed to become superconducting at 100 million K, so these are the real high-T_c champs of the universe.
All in all, these extremes mean that the study of neutron stars affords us some unique glimpses into areas of physics that we couldn't study otherwise.
So, like, how do we get neutron stars?
Neutron stars are believed to form in supernovae such as the one that
formed the Crab Nebula (or check out
this cool X-ray image of the
nebula, from the Chandra X-ray Observatory). The stars that
eventually become neutron stars are thought to start out with about
8 to 20-30 times the mass of our sun. These numbers are probably going
to change as supernova simulations become more precise, but it appears
that for initial masses much less than 8 solar masses the star becomes
a white dwarf, whereas for initial masses a lot higher than 20-30 solar
masses you get a black hole instead (this may have happened with
Supernova 1987A, although
detection of neutrinos in the first few seconds of the supernova suggests
that at least initially it was a neutron star). In any case, the basic idea is
that when the central part of the star fuses its way to iron, it can't
go any farther because at low pressures iron 56 has the highest binding
energy per nucleon of any element, so fusion or fission of iron 56
requires an energy input. Thus, the iron core just accumulates until
it gets to about 1.4 solar masses (the "Chandrasekhar mass"), at which
point the electron degeneracy pressure that had been supporting it
against gravity gives up the ghost and collapses inward.
At the very high pressures involved in this collapse, it is energetically favorable to combine protons and electrons to form neutrons plus neutrinos. The neutrinos escape after scattering a bit and helping the supernova happen, and the neutrons settle down to become a neutron star, with neutron degeneracy managing to oppose gravity. Since the supernova rate is around 1 per 30 years, and because most supernovae probably make neutron stars instead of black holes, in the 10 billion year lifetime of the galaxy there have probably been 10^8 to 10^9 neutron stars formed. One other way, maybe, of forming neutron stars is to have a white dwarf accrete enough mass to push over the Chandrasekhar mass, causing a collapse. This is speculative, though, so I won't talk about it further.
The guts of a neutron star
We'll talk about neutron star evolution in a bit, but let's say you take
your run of the mill mature neutron star, which has recovered from its
birth trauma. What is its structure like? First, the typical mass of
a neutron star is about 1.4 solar masses, and the radius is probably
about 10 km. By the way, the "mass" here is the gravitational mass (i.e.,
what you'd put into Kepler's laws for a satellite orbiting far away).
This is distinct from the baryonic mass, which is what you'd get if you
took every particle from a neutron star and weighed it on a distant scale.
Because the gravitational redshift of a neutron star is so great,
the gravitational mass is about 20% lower than the baryonic mass.
Anyway, imagine starting at the surface of a neutron star and burrowing your way down. The surface gravity is about 10^11 times Earth's, and the magnetic field is about 10^12 Gauss, which is enough to completely mess up atomic structure: for example, the ground state binding energy of hydrogen rises to 160 eV in a 10^12 Gauss field, versus 13.6 eV in no field. In the atmosphere and upper crust, you have lots of nuclei, so it isn't primarily neutrons yet. At the top of the crust, the nuclei are mostly iron 56 and lighter elements, but deeper down the pressure is high enough that the equilibrium atomic weights rise, so you might find Z=40, A=120 elements eventually. At densities of 10^6 g/cm^3 the electrons become degenerate, meaning that electrical and thermal conductivities are huge because the electrons can travel great distances before interacting.
Deeper yet, at a density around 4x10^11 g/cm^3, you reach the "neutron drip" layer. At this layer, it becomes energetically favorable for neutrons to float out of the nuclei and move freely around, so the neutrons "drip" out. Even further down, you mainly have free neutrons, with a 5%-10% sprinkling of protons and electrons. As the density increases, you find what has been dubbed the "pasta-antipasta" sequence. At relatively low (about 10^12 g/cm^3) densities, the nucleons are spread out like meatballs that are relatively far from each other. At higher densities, the nucleons merge to form spaghetti-like strands, and at even higher densities the nucleons look like sheets (such as lasagna). Increasing the density further brings a reversal of the above sequence, where you mainly have nucleons but the holes form (in order of increasing density) anti-lasagna, anti-spaghetti, and anti-meatballs (also called Swiss cheese).
When the density exceeds the nuclear density 2.8x10^14 g/cm^3 by a factor of 2 or 3, really exotic stuff might be able to form, like pion condensates, lambda hyperons, delta isobars, and quark-gluon plasmas. Here's a gorgeous figure (from http://www.astroscu.unam.mx/neutrones/NS-picture/NStar/NStar-I.gif) that shows the structure of a neutron star:
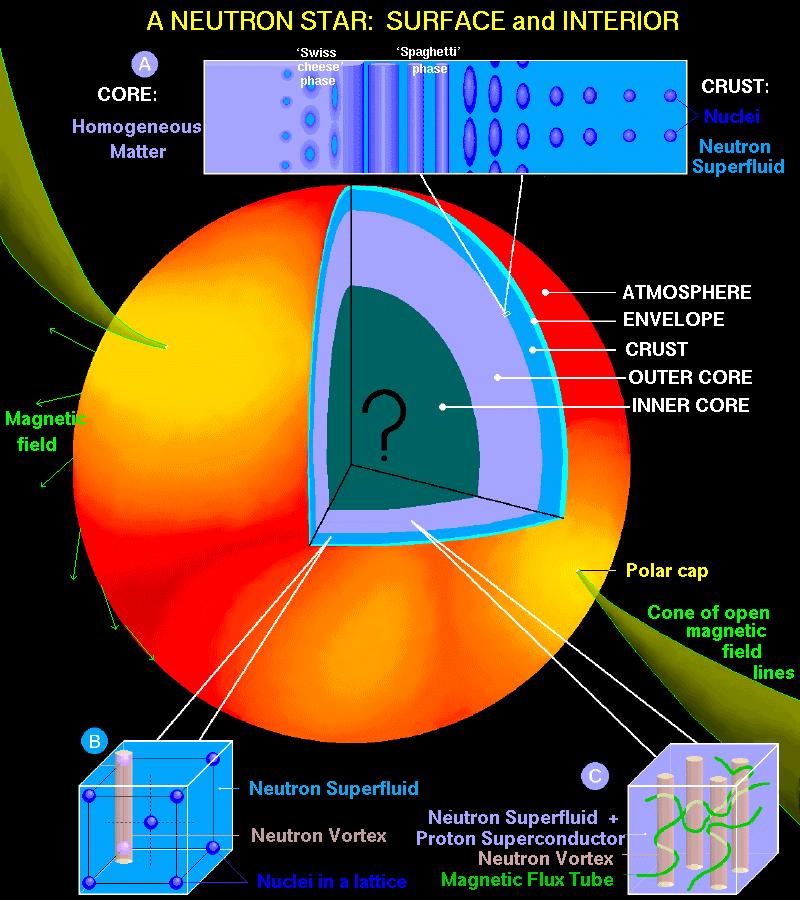
Yes, you may say, that's all very well for keeping nuclear theorists employed, but how can we possibly tell if it works out in reality? Well, believe it or not, these things may actually have an effect on the cooling history of the star and their spin behavior! That's part of the next section.
The decline and fall of a neutron star
Thermal history
At the moment of a neutron star's birth, the nucleons that compose it have energies characteristic of free fall, which is to say about 100 MeV per nucleon. That translates to 10^12 K or so. The star cools off very quickly, though, by neutrino emission, so that within a couple of seconds the temperature is below 10^11 K and falling fast. In this early stage of a neutron star's life neutrinos are produced copiously, and since if the neutrinos have energies less than about 10 MeV they sail right through the neutron star without interacting, they act as a wonderful heat sink. Early on, the easiest way to produce neutrinos is via the so-called "URCA" processes: n->p+e+(nu) [where (nu) means an antineutrino] and p+e->n+nu. If the core is composed of only "ordinary" matter (neutrons, protons, and electrons), then when the temperature drops below about 10^9 K all particles are degenerate and there are so many more neutrons than protons or electrons that the URCA processes don't conserve momentum, so a bystander particle is required, leading to the "modified URCA" processes n+n->n+p+e+(nu) and n+p+e->n+n+nu. The power lost from the neutron stars to neutrinos due to the modified URCA processes goes like T^8, so as the star cools down the emission in neutrinos drops sharply.
When the temperature has dropped far enough (probably between 10 and 10,000 years after the birth of the neutron star), processes less sensitive to the temperature take over. One example is standard thermal photon cooling, which has a power proportional to T^4. Another example is thermal pair bremsstrahlung in the crust, where an electron passes by a nucleus and, instead of emitting a single photon as in standard bremsstrahlung, emits a neutrino-antineutrino pair. This has a power that goes like T^6, but its importance is uncertain. In any case, the qualitative picture of "standard cooling" that has emerged is that the star first cools by URCA processes, then by modified URCA, then by neutrino pair bremsstrahlung, then by thermal photon emission. In such a picture, a 1,000 year old neutron star (like the Crab pulsar) would have a surface temperature of a few million degrees Kelvin.
But it may not be that simple...
Near the center of a neutron star, depending on the equation of state the density can get up to several times nuclear density. This is a regime that we can't explore on Earth, because the core temperatures of 10^9 K that are probably typical of young neutron stars are actually cold by nuclear standards, since in accelerators when high densities are produced it's always by smashing together particles with high Lorentz factors. Here, the thermal energies of the particles are much less than their rest masses. Anyway, that leaves us with only theoretical predictions, which (as you might expect given the lack of data to guide us) vary a lot. Some people think that strange matter, pion condensates, lambda hyperons, delta isobars, or free quark matter might form under those conditions, and it seems to be a general rule that no matter what the weird stuff is, if you have exotic matter then neutrino cooling processes proportional to T^6 can exist, which would mean that the star would cool off much faster than you thought. It even appears possible in some equations of state that the proton and electron fraction in the core may be high enough that the URCA process can operate, which would really cool things down in a hurry. Adding to the complication is that the neutrons probably form a superfluid (along with the protons forming a superconductor!), and depending on the critical temperature some of the cooling processes may get cut off.
So how do we test all this? We expect that after a hundred years or so the core will become isothermal (because it is then superfluid), and we can estimate thermal conductivities in the crust, so if we could measure the surface temperatures of many neutron stars, then we could estimate their core temperatures, which combined with age estimates and an assumption that all neutron stars are basically the same would tell us about their thermal evolution, which in turn would give us a hint about whether we needed exotic matter. Unfortunately, neutron stars are so small that even at the 10^6 K or higher temperatures expected for young neutron stars we can just barely detect them. Adding to the difficulty is that at those temperatures the peak emission is easily absorbed by the interstellar medium, so we can only see the high-energy tail clearly. Nonetheless, ROSAT has detected persistent X-ray emission from several young, nearby neutron stars, so now we have to interpret this emission and decide what it tells us about the star's temperature.
This ain't easy. The first complication is that the X-ray emission might not be thermal. Instead, it could be nonthermal emission from the magnetosphere. That could carry information of its own, but it makes temperature determinations difficult; basically, we have to say that, strictly, we only have upper limits on the thermal emission. Even if it were all thermal, we need to remember that we only see a section of the spectrum that is observable by an X-ray satellite, so we could be fooling ourselves about the bolometric luminosity. In fact, some early simulations of radiation transfer through a neutron star atmosphere indicated that a neutron star of effective temperature T_eff would yield far more observed counts than a blackbody at T_eff. Thus, a blackbody fit would overestimate the true temperature. These simulations used opacities computed for zero magnetic field. Thus, especially for low atomic number elements such as helium, there weren't any opacity sources at 500 eV (where the detectors operate), so in effect we would be seeing deeper into the atmosphere where it was hotter. Such simulations may be relevant for millisecond pulsars, which have magnetic fields in the 10^8 G to 10^10 G range.
Most pulsars, though, have much stronger fields, on the order of 10^12 G. In fields this strong, the binding energies of atoms go up (as mentioned before, the ground state binding energy of hydrogen in 10^12 G is 160 eV), meaning that the opacity at those higher energies rises as well. Thus, the X-ray detectors don't see as far down into the atmosphere, and the inferred temperature is less than in the nonmagnetic case. The details of the magnetic calculations are very difficult to do accurately, as they require precise computations of ionization equilibrium and polarized radiative transfer, and these are nasty in strong fields and dense, hot, matter. It seems, though, that when magnetic effects are included a blackbody isn't too bad an approximation. Stay tuned.
So what does all this mean with respect to neutron star composition?
Yep, you guessed it, we don't have enough data. If you squint and look
sideways at a graph of estimated temperature versus age, you might
convince yourself that there is some evidence of rapid cooling, which
wouldn't fit with the standard cooling scenario. But, unfortunately,
the error bars are too large to be definite. We really need a large
area detector that can pick up more stars. Features in
the spectra would be nice, too, but at the moment that's just a dream.
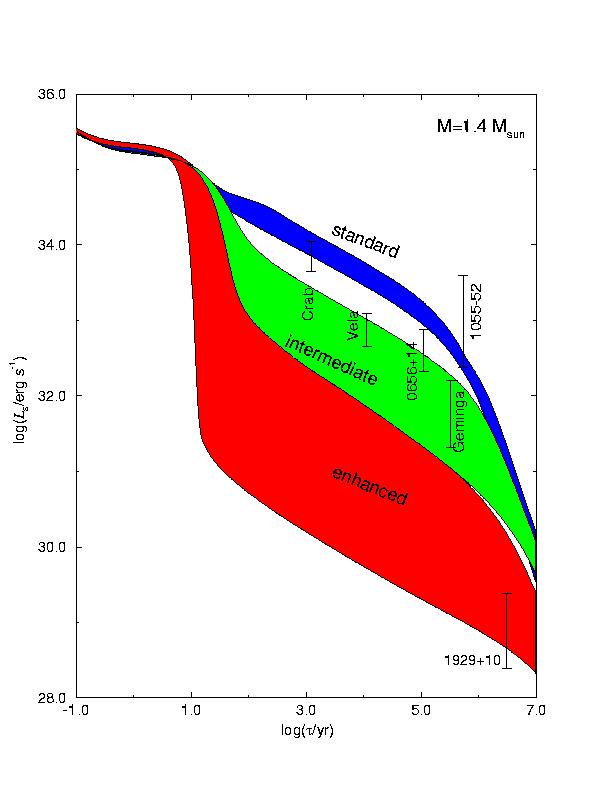
In the meantime, here's some recent data, plotted against several
representative cooling curves that make various assumptions about
the internal composition (this graph is from
www.physik.uni-muenchen.de/sektion/suessmann/astro/cool/:
Neutron stars rotate very rapidly, up to 600 times per second. But how
are they spinning when they are born?
They may be born rotating very fast, with periods comparable to a
millisecond (although evidence is ambiguous). After that,
they spin down ever after because of magnetic
torques. This seems to be supported by the fact that some of the
youngest pulsars, such as the Crab pulsar (33 ms) and the Vela pulsar
(80 ms) have unusually short periods. After a pulsar is born,
its magnetic field will exert a torque and slow it down, with
typical spindown rates of 10^-13 s/s for a young pulsar like the Crab.
Although overall the tendency is for isolated pulsars to slow down, they
can undergo very brief periods of spinup. These events are called
"glitches", and they can momentarily change the period of a pulsar by
up to a few parts in a million. The effects of glitches decay away
in a few days, and then the pulsar resumes its normal spindown. In
current models of glitches, the superfluid core and normal crust are
presumed to couple impulsively, and since the crust had been spun down
by the magnetic field while the superfluid kept rotating at its original
rate, this coupling would speed up the crust, leading to the observed
spinup. It is very difficult to treat this process from first (nuclear)
principles, because the critical angular velocity difference at which
the crust and superfluid finally couple depends sensitively on various
ill-determined properties of neutron superfluids, and since these
properties aren't directly accessible by experiments we may have to be
satisfied by our current phenomenological description. Incidentally,
the glitch should also heat up the crust, and late in the lifetime of
the neutron star heating by rotational dissipation can actually become
a significant source of heat and affect the temperature evolution.
Fine, so that's an isolated neutron star. If the star has a companion,
it can accrete from the companion and have its rotational frequency
altered that way. If the companion is a low-mass star, say half the
mass of our Sun or lower, accretion tends to proceed by Roche lobe
overflow (more on that later). This type of flow has a lot of angular
momentum, so the matter forms a disk around the star. The radius of the
inner edge of the disk is determined by the strength of the magnetic
field; the stronger the field, the farther out it can control the
accretion flow (for a given accretion rate). The star then (more or less)
tries to come to equilibrium with the Keplerian angular velocity of the
matter at the inner edge of the accretion disk. This means that neutron
stars with relatively small (10^8 to 10^9 Gauss) magnetic fields can be
spun up to high frequencies, and this is the accepted picture of how
we get millisecond pulsars.
If the companion of the neutron star is a high-mass star (over 10 solar
masses) instead, then the matter that makes it onto the neutron star
goes in the form of a low angular momentum wind. Therefore, the neutron
star isn't spun up to such high frequencies; in fact, some pulsars that
are in high-mass systems have periods longer than 1000 seconds. The
process of wind accretion is a very complicated one, and numerical
simulations of the process push the limits of computers. It appears that,
in some circumstances, a disk may form briefly around the neutron star,
only to be dissipated and replaced by a disk going the other way. One
barrier to understanding this kind of accretion is that, even with
today's computers, high-resolution 3D simulations just aren't feasible
now, so we have to derive what insight we can from good two-dimensional
calculations.
This changed dramatically in 1967, due to serendipity and the
diligence of an Irish graduate student by the name of Jocelyn
Bell. Bell and her advisor, Anthony Hewish, were working on radio
observations of quasars, which had been discovered in 1963. Bell
and some other graduate students constructed a scintillation array
for the observations, then she got down to examining the charts of
data produced (she had to analyze the miles of charts by hand, since
this was in the days before powerful computers!). One day she
noticed a bit of "scruff" that appeared on the charts every second
and a third. The scruff was so regular that she first thought it
must be artificial. However, careful checking showed that indeed
the signal was extraterrestrial, and in fact that it must be from
outside the solar system. This source, CP 1919, was the first
radio pulsar to be discovered.
The discovery initiated a storm of activity that has still not
abated. A number of other pulsars were discovered, including one
in the Crab Nebula, site of a famous supernova in the year 1054
that was observed by Chinese, Arabic, and North American astronomers
(but not recorded, as far as we know, by Europeans). Within a
year or so of the initial discovery, it became clear that (1)
pulsars are fast, with periods known in 1968 from 0.033 seconds
(the Crab pulsar) to about 2 seconds, (2) the pulsations are
very regular, with a typical rate of change of only a second
per ten million years, and (3) over time, the period of a pulsar
always increased slightly.
With this data, it was realized quickly that pulsars had to be
rotating neutron stars. With certain exceptions that don't apply
in this case, if a source varies over some time t, then
its size must be less than the distance light can travel in that
time, or ct (otherwise the variation would be happening
faster than the speed of light). Thus, these objects had to
be less than 300,000 km/s times 0.033 seconds, or 10,000 km, in
size. This restricts us to white dwarfs, neutron stars, or black
holes. You can get a periodic signal from such objects via
pulsation, rotation, or a binary orbit. White dwarfs are large
enough that their maximum pulsational, rotational, or orbital
frequencies are more than a second, so this is ruled out. Black
holes don't have solid surfaces to which to attach a beacon, so
rotation or vibration of black holes is eliminated. Black holes
or neutron stars in a binary could produce the required range of
periods, but the binary would emit gravitational radiation, the
stars would get closer together, and the period would decrease,
not increase (and would do so very quickly, too!). Pulsations of
neutron stars typically have periods of milliseconds, not seconds.
The only thing left is rotating neutron stars, and this fits all
of the observations admirably. Here's an
animated gif of a pulsar.
There have now been more than 1000 radio pulsars discovered, with
periods from about 1.4 milliseconds to more than 5 seconds. Their
discovery is considered one of the three most important
astronomical discoveries in the latter half of the twentieth
century (along with quasars and the microwave background), and
in part for his role in the discovery of pulsars Anthony Hewish
shared the 1974 Nobel Prize in physics.
If the companion star has less than the mass of our Sun, the
mass transfer occurs via Roche lobe overflow. If part of the
companion star's envelope is close enough to the neutron star,
the neutron star's gravitational attraction on that part of
the envelope is greater than the companion star's attraction,
with the result that the gas in the envelope falls onto the
neutron star. However, since the neutron star is tiny, astronomically
speaking, the gas has too much angular momentum to fall on the
star directly and therefore orbits around the star in an accretion
disk. Within the disk, magnetic or viscous forces operate to
allow the gas in the disk to drift in slowly as it orbits, and
to eventually reach the stellar surface. If the magnetic field
at the neutron star's surface exceeds about 10^8 G, then before
the gas gets to the stellar surface the field can couple strongly
to the matter and force it to flow along field lines to the
magnetic poles. The friction of the gas with itself as it spirals
in towards the neutron star heats the gas to millions of degrees,
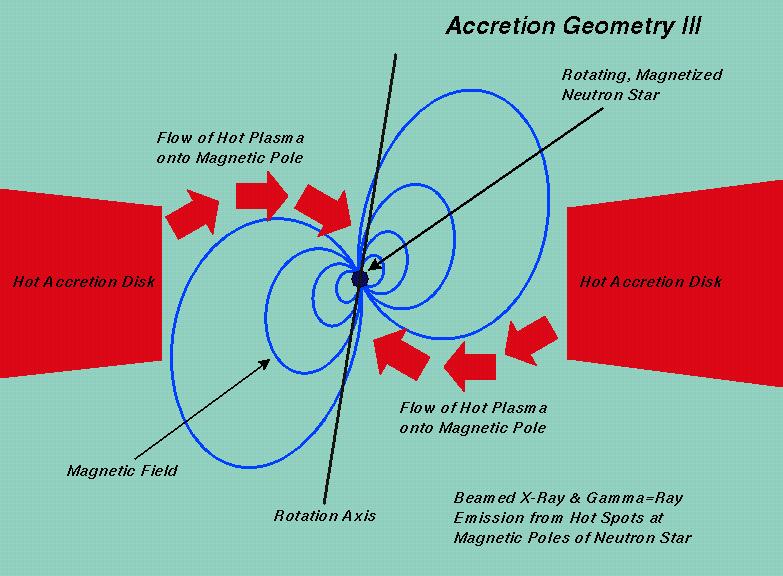
and causes it to emit X-rays. Some characteristic dimensions of
this sort of system are displayed in the figure.
Here, from
wwwastro.msfc.nasa.gov/xray/openhouse/ns/, is a cartoon of
the inner region where the neutron star's magnetic field controls
matter:
Neutron stars in these kind of systems are believed to have
surface magnetic fields between 10^7 and 10^10 Gauss. This
means that the accreting gas can spiral very close to the
neutron star before it is grabbed by the magnetic field. At
such a close distance, the orbital frequency is very high
(hundreds of Hertz), so the neutron star is spun up rapidly.
As mentioned earlier, this is how we think we get millisecond
pulsars. Those millisecond pulsars, by the way, are extremely
stable rotators; the best are at least as stable as atomic
clocks! There have been suggestions that using millisecond
pulsars as cosmic clocks could tell us about all sorts of
exotic things, such as the presence of a background of gravitational
radiation left over from the Big Bang.
Another fun phenomenon associated with neutron stars that have
low-mass companions is X-ray bursts. These typically last
a few seconds to a few minutes, and have a peak luminosity
nearly a hundred thousand times our Sun's luminosity. The
model for these bursts is that as hydrogen and helium is
tranferred to the neutron star from the companion, it builds
up in a dense layer. Eventually, the hydrogen and helium have
been packed in a layer so dense and hot that thermonuclear
fusion starts, which then converts most or all of the gas into
iron, releasing a tremendous amount of energy. This is the
equivalent of detonating the entire world's nuclear arsenal
on every square centimeter of the neutron star's surface within
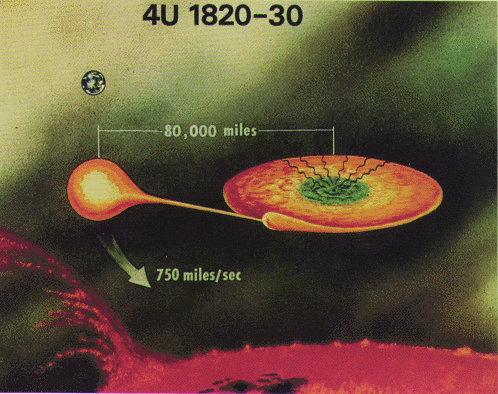
a minute! Some of these binaries can be amazingly close to one
another. Here's an artist's conception (from
heasarc.gsfc.nasa.gov/Images/exosat/slide_gifs/exosat18.gif)
of one particularly extreme case, that of 4U~1820-30, which has
a binary period of just over eleven minutes! Too bad the distances
are in miles...
If the companion to the neutron star has a mass between one and
ten times our Sun's mass, the mass transfer is unstable and
doesn't last very long, so there are few objects in this category.
If the companion to the neutron star has a mass more than about
ten times our Sun's mass, the companion naturally produces a
stellar wind, and some of that wind falls on the neutron star.
The neutron stars in these systems have strong magnetic fields,
around 10^12 Gauss (similar to typical isolated pulsars). At
field strengths this high, almost all the accreting gas is
forced to flow along field lines to the magnetic poles. This
means that the X-rays primarily come from the resulting hot
spots on the poles. It also means that if the magnetic axis
and rotation axis of the star aren't co-aligned, the radiation
sweeps past us once per rotation and we see X-ray pulsations.
These systems are therefore called "accretion-powered pulsars",
to distinguish them from the "rotation-powered pulsars" that
Jocelyn Bell discovered.
For some recent results on accreting neutron stars, check out
a
poster from a science
fair for grownups held at the University of Chicago.
Loosely speaking, gamma-ray bursts are, well, bursts of energy that
appear mostly in gamma rays and come from outside the Earth. The flux
at earth is between 10^-8 erg/cm^2/s and 10^-3 erg/cm^2/s, the duration
of the bursts is between 10 ms and 1000 s, and the photons typically have
energies between 100 keV and 2 MeV, although energies down to 5 keV and
up to 18 GeV have been seen from some bursts. The flux as a function of
time varies from burst to burst, but often a spike within a burst follows
the "fred" profile (fast rise, exponential decay). Here's an
animated gif showing a simulation of
a burst as we'd see it on a map of the Galaxy (left) and its brightness
as a function of time (right). All in all, gamma-ray
bursts are extremely heterogeneous, so it is tough to extract characteristic
behaviors that would lead to easy classification (see a typical
time profile for a GRB).
Can we at least tell how far away gamma-ray bursts are? Until recently,
the answer was "no", not with any certainty.
From the early 1970s it has been apparent that
gamma-ray bursts come from all parts of the sky with approximately equal
probability. Since other aspects of gamma-ray bursts (such as the fast
rise time [<1 ms in some cases] and high photon energies) seemed consistent
with a neutron star origin, most people prior to 1990 believed that
gamma-ray bursts came from galactic neutron stars, and that instruments
simply hadn't had the sensitivity to probe deeply enough to see a bias
towards the galactic center and plane. However, since 1990 the Burst
and Transient Source Experiment (BATSE) aboard the Compton Gamma-Ray
Observatory has seen nearly one gamma-ray burst per day, and these too
are nearly isotropic (click for the sky map
of the first 921 bursts).
It is believed that, if galactic neutron stars
really are the sources of gamma-ray bursts, BATSE should be able to see
them far enough away that the distribution should be more like a pancake
than a sphere. Another piece of evidence comes from the number of
sources seen with at least a given flux. If the universe were Euclidean
and the sources were spread out uniformly, then out to a distance r
there would be a number of sources proportional to r^3, and the dimmest
sources would have fluxes proportional to 1/r^2. Thus, in a Euclidean
universe with uniformly distributed sources of a given intrinsic
luminosity, a plot of log N (N=number of sources at a flux greater than
F) versus log F should have a slope of -3/2. At the highest fluxes this
slope is seen, but at lower fluxes the slope becomes smaller, exhibiting
a continuous rollover and becoming about -0.8 at the lowest fluxes
BATSE can see.
What does that mean? The dropoff at lower fluxes, which corresponds to
greater distances if the intrinsic luminosity is constant, means that in
some sense there is an edge to the distribution. For example, if the
sources were distributed in a thin plane instead of a sphere, the slope
would be -1, and for sources in a line the slope is -0.5. Even if the
source distribution is spherical, the slope will roll over if the sources
become less dense at greater distances, or if the flux drops off faster
than 1/r^2. Because of the isotropy of the distribution, many people
believed that gamma-ray bursts are cosmological, at typical redshifts
z=1, where the redshift would decrease the flux in about the right
way to account for the log N - log F rollover. But until 1997 there
wasn't any "smoking gun" to tell us for sure that the bursts were
cosmological, and actually there were plausible models of gamma-ray
bursts in which the bursts came from an extended halo around our own
galaxy.
All this changed in 1997, when researchers using the Italian-Dutch
satellite BeppoSAX made a tremendous breakthrough. A sticking point
in our understanding of gamma-ray bursts was that they were always a
"one and done" type of phenomenon, in which, after a brief flash of
gamma-rays lasting a few seconds, that was all she wrote. The lack
of any detectable emission in other frequencies (such as optical and
radio) meant that these sources couldn't be localized with any
certainty. This is where BeppoSAX came in. This satellite has the
capability of detecting X-ray emission from half a dozen to a dozen
gamma-ray bursts per year and localizing the emission to within
about two arcminutes (a thirtieth of a degree, or a little less
than the apparent size of a billiard ball at the far end of a
football field). This is about 100 times better than the localization
possible with BATSE. It allowed people to discover that most
of the gamma-ray bursts observed with BeppoSAX have x-ray afterglows;
here's an image of the first one, showing
a bright spot (left) that fades away later (right). Many have
optical and radio afterglows as well! The afterglows
in optical and radio allowed the position to be nailed down to an
arcsecond or better (the apparent size of an eyelash at the far end
of a football field!). Further observations showed that, at least
in projection and probably in reality, the gamma-ray bursts are in
galaxies. Not only that, but redshifts have been measured for many
of these galaxies, and some of them are really big: one was measured
at a redshift greater than 3.4! So that settles at least part of
the question: the bursts observed with BeppoSAX are definitely
cosmological.
If gamma-ray bursts are cosmological, their energy release must be
gigantic. It is now thought that most bursts are tightly beamed
(like a lighthouse) and emit a good 10^51 ergs in just gamma rays.
It is still really puzzling how this could happen. The
constraints on these models are really tight, and no detailed model
yet suggested can circumvent all the constraints. No
matter what these are, though, the energy release by itself guarantees
that the central engine is one of the biggest blasts around! The
two most popular current ideas are (1) the bursts are caused by the
inspiral and merger of two neutron stars or a neutron star and a black
hole, or (2) the bursts are caused by the collapse of a massive star
(maybe 20 solar masses or more) into a rapidly spinning massive black
hole. General opinion is that the longer bursts are of type (2), but
there is still a question about the shorter bursts. Either way, it
seems unavoidable that all that energy sails out into interstellar
space and produces a serious blast wave.
One particular burst from SGR 0525-66, which occurred on March 5,
1979, has attracted so much attention that it is usually called
just the "March 5 event". This was the highest intensity gamma-ray
event seen up to that point. It started with a hard spike that
lasted a quarter of a second and had a rise time less than a
millisecond, then continued emitting softer radiation for another
200 seconds. The emission during this extended tail had a clear
period of 8 seconds, and was consistent with rotational modulation.
Because of the high intensity and rapid onset of this event,
nine different satellites throughout the Solar System recorded this
event, and the relative timing between the satellites allowed the
direction of the event to be determined very accurately. It was
determined that the event came from a direction consistent with
the N49 supernova remnant in the Large Magellanic Cloud, putting
it at a distance of somewhat more than 50 kiloparsecs. At this
distance, the initial hard spike had a peak luminosity of more
than 10^45 ergs per second. That is to say, in the first quarter
second of the burst, this source put out as much energy as the
Sun radiates in 3000 years! This is also the event that makes
some astronomers think that SGRs are related to classical
gamma-ray bursts. If the hard spike is analyzed by itself, then
its duration, light curve, and energy spectrum are indistinguishable
from classical GRBs. Indeed, if the event had occured ten times
as far away as it did (so that we would have missed the extended
soft emission), we would have considered this another ho-hum
gamma-ray burst.
Observations of other bursts from SGR 0525-66 (none as spectacular
as the March 5 event) and bursts from SGR 1900+14 and SGR 1806-20
suggested initially that all are associated with supernova remnants,
but as mentioned above this has been challenged. Even if they are
associated with the remnants, the sources
are not at the center of the remnants; instead, they are
off to the side, by distances that would imply a velocity of 500-1500
kilometers per second. The typical peak luminosity of a SGR burst
is 10^40 to 10^42 ergs per second. This information can be put
together as follows:
Thus, if SGRs are associated with supernova remnants then they
come from young neutron stars. The next question is
what is the energy source for the bursts? One naturally thinks
of accretion or rotation, but strong magnetic fields have also
been considered.
If SGRs are associated with supernova remnants they are moving
at high speeds, because they are not at the center of the
remnants. Accretion then has serious problems, because the
high velocities inferred for all three SGRs mean that the neutron
star can't pick up enough mass from the interstellar medium. Also,
it turns out that accretion from, e.g., asteroids would be
expected to last tens of thousands of seconds instead of the
observed tenths of seconds. Rotation has even greater problems.
A neutron star spinning at an 8 second period, such as the one
that produced the March 5 event, has only about 3 times 10^44
ergs in rotational energy available. But the March 5 event itself
released about 4 times 10^44 ergs, and the X-ray energy
released since then in persistent emission is another 3 times
10^44 ergs, so there isn't enough rotational energy to do the job.
Starting about 1992, Chris Thompson and Rob Duncan started proposing
another energy source, that of very strong magnetic fields. They
were drawn to this in part because the March 5 event implies a
very long rotational period (8 seconds) compared to the expected
birth spin period of neutron stars (less than a second). If, as
usually thought, the neutron star spins down by magnetic braking,
then to get to that long period in the 5,000 year age of the N49
supernova remnant requires that the field be nearly 10^15 Gauss!
Thompson and Duncan noticed that this would imply a total magnetic
energy in the star of about 10^47 ergs, which is easy enough.
They also found that this model is consistent with the other
properties of SGR bursts.
So, maybe some neutron stars have magnetic fields of 10^15 Gauss.
So what? Given that we're sure that some neutron stars have fields
of 10^12 to 10^13 Gauss, which already sounds unbelievably large,
what's the big deal with another two orders of magnitude?
The difference comes at the subatomic level. In a magnetic field,
a charged particle such as an electron or proton will spiral
around the field at a preferred frequency, the cyclotron
frequency, that is proportional
to the strength of the field. This principle is used in
magnetic resonance imaging, where the preferred frequency (of
nuclei) is in the radio wavelengths. When magnetic fields of
neutron star strength are introduced, the electron cyclotron
frequency is in the X-rays, and when the field is
4.414 times 10^13 Gauss the electron cyclotron energy (the
cyclotron frequency times Planck's constant) equals
the electron rest mass energy. This field turns out to be
a critical field in quantum electrodynamics, such that (essentially)
above that field there are a number of bizarre processes (e.g.,
single photon pair production, photon splitting) that can be
very important, whereas below the critical field those processes
are negligible. We don't have a prayer of accessing this regime
of ultrastrong fields in the laboratory, and we only have our
quantum mechanical predictions to guide us. So, if we can
establish that such fields exist in astronomy, then by studying
those objects we can test our quantum mechanical theories in a
new physical regime.
But first, we have to get more direct evidence that such high
fields exist. Recent supporting evidence arrived in 1998, when
several soft gamma-ray repeaters were active and when it was
finally possible to measure (1) a spin period and (2) a rate of
change of the spin period, which in the simplest approximation
allow an estimate of the magnetic field of these sources. You
guessed it, it seems like magnetic fields greater than about 10^14
Gauss are required, although there are still some subtleties.
What would really be nice would be a signature in the energy
spectrum of these ultrastrong fields. We don't have it yet,
but there has been a lot of effort by many people.
Tomek Bulik and I have proposed the one that I think is most
promising. It relates to something called the vacuum resonance,
and the spectral signature is a dip in the X-ray spectrum that
moves to lower energies when the intensity is higher. If such
a signature is seen, we will then have strong and direct evidence
for the existence of these superstrong fields, and theorists such
as myself will have a wonderful new playground!
Misanthropic (aka isolated) neutron stars
Neutrons were discovered in 1932, and very shortly afterward (in 1934)
a suggestion was made by Walter Baade and Fritz Zwicky that neutron
stars were formed in supernovae. But for many decades after that,
neutron stars were just hypothetical phenomena that didn't attract
much interest. Since the stars are so small, people felt that the
prospects for observing them were minimal, and thus little effort
was expended on theory or observation of neutron stars.Social (aka accreting) neutron stars
Not all neutron stars are destined to lead a life of isolation.
Some of them are born in binaries that survive the supernova
explosion that created the neutron star, and in dense stellar
regions such as globular clusters some neutron stars may be able
to capture companions. In either case, mass may be transferred
from the companion to the neutron star, as mentioned in the
spin evolution section above.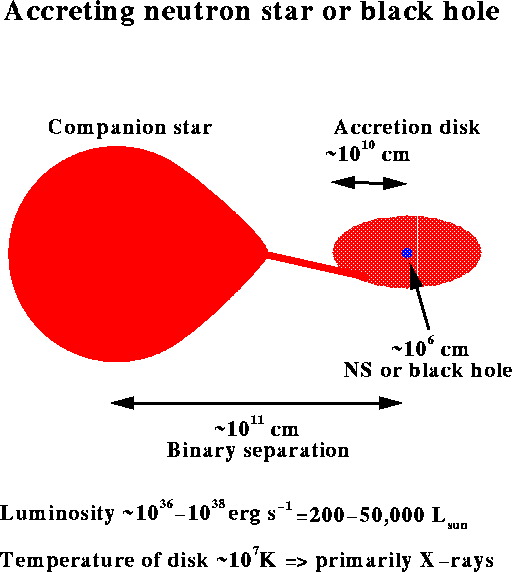
What the @#$% makes gamma-ray bursts?
Gamma-ray bursts have been known for more than 25 years, but there are
still a lot of uncertainties about their origins. They were
first discovered in the late 1960's as part of nuclear test ban verification;
US satellites picked up bursts of gamma rays and there was a lot of
concern that these might be due to Soviet nuclear explosions, but it
was determined that the bursts originated outside the atmosphere. The
"official" discovery came in 1973 (by Klebsedal, Olsen, and Strong).
Since then, more than 2500 bursts have been detected, over 1800 by
BATSE (the Burst and Transient Source Experiment aboard the Compton
Gamma-Ray Observatory). Before tackling the
question of what gamma-ray bursts are, we need to establish
what they are observationally.Soft gamma-ray repeaters and whopping magnetic
fields
Another (somewhat less) mysterious type of bursting events believed
to come from neutron stars is the soft gamma-ray repeater bursts.
These typically last from 0.1 seconds to 3 seconds and have spectral
peaks in the 10 keV to 30 keV range.
Soft gamma-ray repeaters have in the past been identified with
supernova remnants, but with the possible exception of
the single source in the Large
Magellanic Cloud (SGR 0525-66) these identifications are now considered
dubious (see Gaensler et al. 2001, ApJ, 559, 963).
Caution is especially appropriate because there
are only four (!) SGRs known (SGR 0525-66, SGR 1900+14,
SGR 1806-20, and SGR 1627-41, where the numbers give the right ascension and
declination in B1950 coordinates). Despite the paucity of these
sources, interest has focused on them because (1) they have
observational properties distinct from that of any other known
astronomical phenomenon, (2) they have some tantalizing links to
gamma-ray bursts, and (3) one current model of SGRs
involves neutron stars with 10^14 Gauss to 10^15 Gauss surface
magnetic fields, in which a variety of exotic microphysical
processes could be important.
Send me to:
 research page
research page